
Solved 1 Prove That If Aв Z Then 4в A2 1 2 Let X Be A Chegg ( [15]) let a1=1 and an 1=2 an. (a) prove that if an<2 then an 1<2. (b) prove that if an>an−1 then an 1>an. (c) using (a) and (b) to find the limit. just list the properties used, do not need a rigorous proof for (c). Question: prove that if. an = {a1 = 1 an 1 = 1 1 1 an then an converges, and then find limn → ∞an. i found that limn → ∞an = √2, and that 1 ≤ an <2, but the convergence seems difficult. my idea is to show that a2n is decreasing, and a2n − 1 is increasing, but i don’t see how. i’d be thankful for any hint.
Solved Prove 1 1 2 Math Find 𝑎 (𝑛 1) an, for n = 1,2,3,4,5, lets first calculate a1 , a2 , a3 , a4 , a5 & a6 it is given that a1 = 1 a2 = 1 for a3 , a4 , a5 & a6 we need to use an = an–1 an–2 , n > 2 an = an 1 an 2 , n > 2 putting n = 3 in (1) a3 = a3 – 1 a3 – 2 = a2 a1 = 1 1 = 2 putting n = 4 in (1) a4 = a4 – 1 a4 – 2 a4 = a3 a2 = 2. Question: let 1 ≤a1 ≤a2 ≤2 and an 2 = √an 1an for n ∈n. (a) (10 marks) prove that an 1 an ≥ 1 2 for all n ∈n. (b) (15 marks) using (a), or otherwise, prove that for n > 1, |an 1 −an| ≤ 2 3 |an −an−1| and hence {an} converges. Let a1 = b1 = 1, an = an–1 2 and bn = an bn–1 for every natural number n ≥ 2. then 15 ∑ n=1 an. bn ∑ n = 1 15 a n. b n is equal to . 4. ( (15]) let a1=1 and an 1=2 an. (a) prove that if an<2 then an 1<2. (b) prove that if an>an−1 then an 1>an. (c) using (a) and (b) to find the limit. just list the properties used, do not need a rigorous proof for (c). your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.
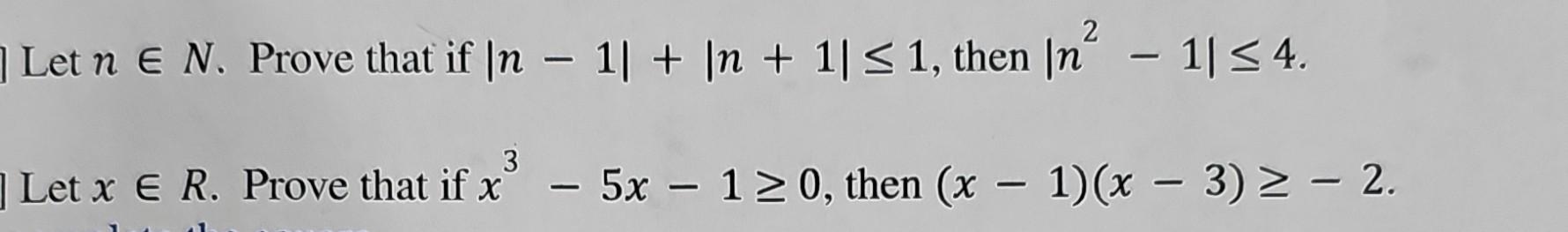
Solved Let Nтииn Prove That If тигnтит1тиг тигn 1тигтйд1 Then Chegg Let a1 = b1 = 1, an = an–1 2 and bn = an bn–1 for every natural number n ≥ 2. then 15 ∑ n=1 an. bn ∑ n = 1 15 a n. b n is equal to . 4. ( (15]) let a1=1 and an 1=2 an. (a) prove that if an<2 then an 1<2. (b) prove that if an>an−1 then an 1>an. (c) using (a) and (b) to find the limit. just list the properties used, do not need a rigorous proof for (c). your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. If we can show that 1 2 s and also that whenever a 2 s, we have also a 1 2 s, then (2) implies that s = n, so that p(n) is true for all n 2 n. let's do a proof from this interpretation. It is given that a1 = 1, for a2 and onward we use this formula. an = an – 1 2 for n ≥ 2 putting n = 2 in (1) a2 = a2 – 1 2. First, it is easy to check the initial condition: \ (a 1\) should be \ (2^1 1\) according to our closed formula. indeed, \ (2^1 1 = 3\text {,}\) which is what we want. to check that our proposed solution satisfies the recurrence relation, try plugging it in. that's what our recurrence relation says! we have a solution. Prove that 12 22 ··· n2=1 6 n(n 1)(2n 1) for all n ∈ n. put f(n) = n(n 1)(2n 1) 6. then f(1) = 1, i.e the theorem holds true for n = 1. to prove the theorem, it suffices to assume that it holds true for n = m and derive it for n = m 1, m = 1,2,3, . we have f(m 1)− f(m) = 1 6 (m 1)[(2m 3)(m 2)− m(2m 1)] = 1 6 (m 1)(6m 6) = (m 1)2.
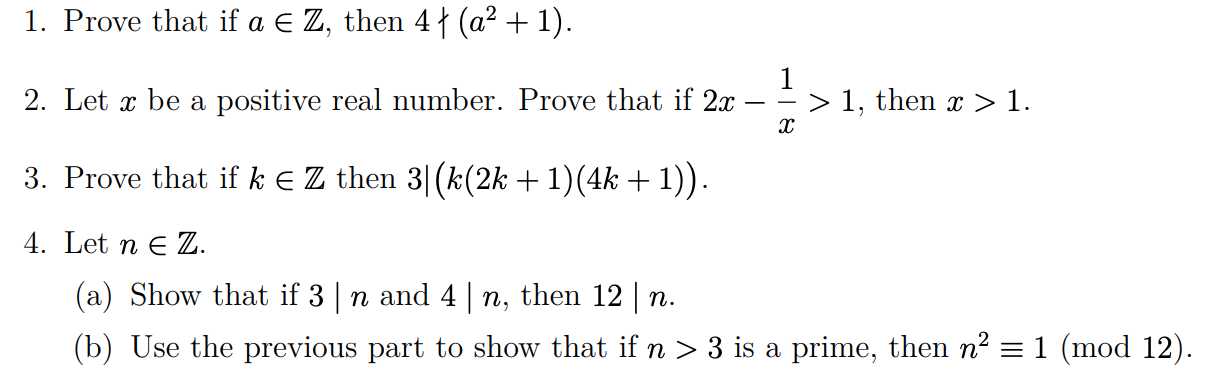
Solved 1 Prove That If Aв Z Then 4в A2 1 2 Let X Be A Chegg If we can show that 1 2 s and also that whenever a 2 s, we have also a 1 2 s, then (2) implies that s = n, so that p(n) is true for all n 2 n. let's do a proof from this interpretation. It is given that a1 = 1, for a2 and onward we use this formula. an = an – 1 2 for n ≥ 2 putting n = 2 in (1) a2 = a2 – 1 2. First, it is easy to check the initial condition: \ (a 1\) should be \ (2^1 1\) according to our closed formula. indeed, \ (2^1 1 = 3\text {,}\) which is what we want. to check that our proposed solution satisfies the recurrence relation, try plugging it in. that's what our recurrence relation says! we have a solution. Prove that 12 22 ··· n2=1 6 n(n 1)(2n 1) for all n ∈ n. put f(n) = n(n 1)(2n 1) 6. then f(1) = 1, i.e the theorem holds true for n = 1. to prove the theorem, it suffices to assume that it holds true for n = m and derive it for n = m 1, m = 1,2,3, . we have f(m 1)− f(m) = 1 6 (m 1)[(2m 3)(m 2)− m(2m 1)] = 1 6 (m 1)(6m 6) = (m 1)2.

Solved 15 Let A1 1 And An 1 2 An A Prove That If An First, it is easy to check the initial condition: \ (a 1\) should be \ (2^1 1\) according to our closed formula. indeed, \ (2^1 1 = 3\text {,}\) which is what we want. to check that our proposed solution satisfies the recurrence relation, try plugging it in. that's what our recurrence relation says! we have a solution. Prove that 12 22 ··· n2=1 6 n(n 1)(2n 1) for all n ∈ n. put f(n) = n(n 1)(2n 1) 6. then f(1) = 1, i.e the theorem holds true for n = 1. to prove the theorem, it suffices to assume that it holds true for n = m and derive it for n = m 1, m = 1,2,3, . we have f(m 1)− f(m) = 1 6 (m 1)[(2m 3)(m 2)− m(2m 1)] = 1 6 (m 1)(6m 6) = (m 1)2.
