
Solved Use Integration By Parts To Evaluate Each Of The Chegg Solve the problem in two steps. start with indefinite integral, find antiderivative using integration by parts. then evaluate antiderivative. you are required to write u, du, dv, v and to write the solution of the problem. (x 1)e* dx solution. step 1: find indefinite integral using. your solution’s ready to go!. In this comprehensive video tutorial, we delve into the concept of integration by parts, a fundamental technique in calculus used to evaluate the integral of products of functions. we'll.

Solved 7 1 Integration By Parts Problem 2 1 Point Use Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: 2. use integration by parts to evaluate the integral. a) ∫xe−xdx b) ∫x2e3xdx c) ∫xsecxtanxdx (hint: ∫secxtanxdx=secx c ) d) ∫x2cosxdx e) ∫tan−1xdx (h int :dxd (tan−1x)=1 x21) f) ∫xlnxdx g) ∫sinxlncosxdx h) ∫csc3xdx i) ∫x (2x 3)99dx j) ∫ (lnx)2dx. Evaluate the integral using integration by parts. ∫x2exdx (use symbolic notation and fractions where needed. use c for the arbitrary constant. absorb into c as much as possible.) ∫x2exdx= your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Use integration by parts, together with the techniques of this section, to evaluate the integral. ∫ ln (x^2 x 2)dx. (25 points) evaluate the following integral: ∫12x2−1ln(x)dx your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.

Solved 1 Point Use Integration By Parts To Evaluate The Chegg Use integration by parts, together with the techniques of this section, to evaluate the integral. ∫ ln (x^2 x 2)dx. (25 points) evaluate the following integral: ∫12x2−1ln(x)dx your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Free online by parts integration calculator integrate functions using the integration by parts method step by step. Integration by parts is a powerful technique in calculus used to find the integral of a product of two functions. it’s essentially the reverse of the product rule for differentiation. the following figures give the formula for integration by parts and how to choose u and dv. scroll down the page for more examples and solutions. For integration by parts, we use the formula \( \int u \, dv = uv \int v \, du \). here, we let \( u = x^5 \) and \( dv = \sqrt{x^3 4} \, dx \). we choose \( u \) as \( x^5 \) because its derivative will decrease the power, making it simpler, and \( dv \) as \( \sqrt{x^3 4} \, dx \), a more complex function to integrate directly. Evaluate the integral using integration by parts with the indicated choices of u and dv: ∫ 8x² ln x dx; u = ln x, dv = 8x² dx.
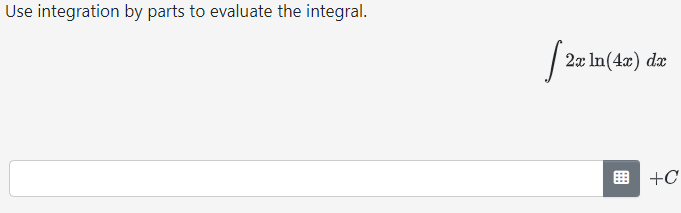
Solved Use Integration By Parts To Evaluate The Chegg Free online by parts integration calculator integrate functions using the integration by parts method step by step. Integration by parts is a powerful technique in calculus used to find the integral of a product of two functions. it’s essentially the reverse of the product rule for differentiation. the following figures give the formula for integration by parts and how to choose u and dv. scroll down the page for more examples and solutions. For integration by parts, we use the formula \( \int u \, dv = uv \int v \, du \). here, we let \( u = x^5 \) and \( dv = \sqrt{x^3 4} \, dx \). we choose \( u \) as \( x^5 \) because its derivative will decrease the power, making it simpler, and \( dv \) as \( \sqrt{x^3 4} \, dx \), a more complex function to integrate directly. Evaluate the integral using integration by parts with the indicated choices of u and dv: ∫ 8x² ln x dx; u = ln x, dv = 8x² dx.
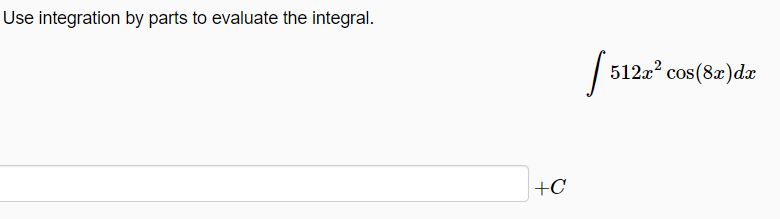
Solved Use Integration By Parts To Evaluate The Integral Chegg For integration by parts, we use the formula \( \int u \, dv = uv \int v \, du \). here, we let \( u = x^5 \) and \( dv = \sqrt{x^3 4} \, dx \). we choose \( u \) as \( x^5 \) because its derivative will decrease the power, making it simpler, and \( dv \) as \( \sqrt{x^3 4} \, dx \), a more complex function to integrate directly. Evaluate the integral using integration by parts with the indicated choices of u and dv: ∫ 8x² ln x dx; u = ln x, dv = 8x² dx.
