
Solved Let S1 And S2 Be Subsets Of A Vector Space V Prove Chegg Let s1 and s2 be subsets of a vector space v over f. show that if s1⊂s2 then span(s1)⊂span(s2) your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. With this definition, if s1 s 1 and s2 s 2 are subsets of a vector space v v such that s1 ⊆s2 s 1 ⊆ s 2, then fs2 ⊆fs1 f s 2 ⊆ f s 1 and then span(s1) ⊆ span(s2) span (s 1) ⊆ span (s 2). finally, the proof of your problem is as goes: proof.

Solved Problem 3 Let V Be A Real Vector Space And Let S1 Chegg Let s 1 and s 2 be subsets of a vector space v. prove that span ( s 1 ∩ s 2 ) ⊆ span ( s 1 ) ∩ span ( s 2 ) . give an example in which span( s 1 ∩ s 2 ) and span ( s 1 ) ∩ span ( s 2 ) are equal and one in which they are unequal. Exercise 1.4.14: show that if s1 and s2 are arbitrary subsets of a vector space v , then span(s1 ∪ s2) = span(s1) span(s2). (the sum of two subsets is defined in the exercises in section 1.3). solution: in order to prove equality of two sets, we need to prove mutual inclu sion. ⊆: let v ∈ span(s1 ∪ s2). Show that, if $s 1$ and $s 2$ are subsets of a vector space $v$ such that $s 1 \subseteq s 2$, then $span(s 1) \subseteq span(s 2)$. A linear combination v = a 1v 1 a mv m, where m is a nonnegative integer, v 1, , v m are elements of s 1 \s 2, and a 1, , a m are scalars. the elements v i lie in s 1, so v 2span(s 1), and they also lie in s 2, so v 2span(s 2) as well. thus, v 2span(s 1) \span(s 2). since v was an arbitrary element of span(s 1 \s 2), we have proved that.

Solved 4 Let V Be A Vector Space And Let S1âš S2 Be Subsets Chegg Show that, if $s 1$ and $s 2$ are subsets of a vector space $v$ such that $s 1 \subseteq s 2$, then $span(s 1) \subseteq span(s 2)$. A linear combination v = a 1v 1 a mv m, where m is a nonnegative integer, v 1, , v m are elements of s 1 \s 2, and a 1, , a m are scalars. the elements v i lie in s 1, so v 2span(s 1), and they also lie in s 2, so v 2span(s 2) as well. thus, v 2span(s 1) \span(s 2). since v was an arbitrary element of span(s 1 \s 2), we have proved that. To show that if s 1 and s 2 are subsets of a vector space v such that s 1 ⊆ s 2 , then span (s 1 ) ⊆ span (s 2 ), we start with definitions. step by step explanation: definitions: the span of a set of vectors is the set of all possible linear combinations of those vectors. if s 1 ⊆ s 2 , this means every element in s 1 is also in s 2 . 5. let s 1 and s 2 be subsets of a vector space v. show that span(s 1[s 2) = span(s 1) span(s 2). solution. [10 points] to show that span(s 1 [s 2) = span(s 1) span(s 2) we show both inclusions. (ˆ): given x 2span(s 1 [s 2), the de nition of span implies that there existp u 1; ;u n 2s 1 [s 2 and a 1; ;a n 2k such that x = n i=1 a iu i. now. Show that if s1 and s2 are arbitrary subsets of a vector space v, then span (s1 union s2) = span (s1) span (s2). can someone solve this? 1. let s1 and s2 be arbitrary subsets of a v. space v. 2. let x be an arbitrary vector such that x belongs to (s1 union s2). so x belongs to s1 or x belongs to s2. Let s1 and s2 be subsets of a vector space v. prove that span (s1∩s2)subespan (s1)∪span (s2). give an example in which span (s1∩s2) and span (s1)∩span (s2) are equal and one in which they are unequal. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.

Solved Let S1 And S2 Be Subsets Not Necessarily Subspaces Chegg To show that if s 1 and s 2 are subsets of a vector space v such that s 1 ⊆ s 2 , then span (s 1 ) ⊆ span (s 2 ), we start with definitions. step by step explanation: definitions: the span of a set of vectors is the set of all possible linear combinations of those vectors. if s 1 ⊆ s 2 , this means every element in s 1 is also in s 2 . 5. let s 1 and s 2 be subsets of a vector space v. show that span(s 1[s 2) = span(s 1) span(s 2). solution. [10 points] to show that span(s 1 [s 2) = span(s 1) span(s 2) we show both inclusions. (ˆ): given x 2span(s 1 [s 2), the de nition of span implies that there existp u 1; ;u n 2s 1 [s 2 and a 1; ;a n 2k such that x = n i=1 a iu i. now. Show that if s1 and s2 are arbitrary subsets of a vector space v, then span (s1 union s2) = span (s1) span (s2). can someone solve this? 1. let s1 and s2 be arbitrary subsets of a v. space v. 2. let x be an arbitrary vector such that x belongs to (s1 union s2). so x belongs to s1 or x belongs to s2. Let s1 and s2 be subsets of a vector space v. prove that span (s1∩s2)subespan (s1)∪span (s2). give an example in which span (s1∩s2) and span (s1)∩span (s2) are equal and one in which they are unequal. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.
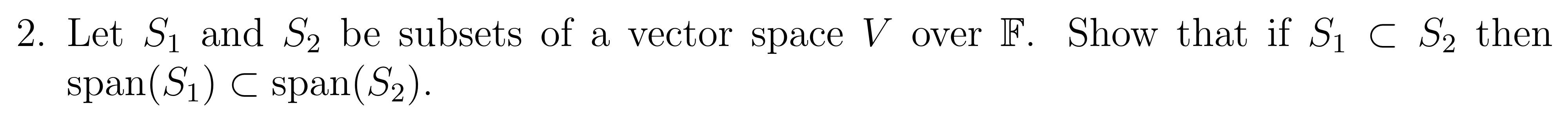
Solved 2 Let S1 And S2 Be Subsets Of A Vector Space V Over Chegg Show that if s1 and s2 are arbitrary subsets of a vector space v, then span (s1 union s2) = span (s1) span (s2). can someone solve this? 1. let s1 and s2 be arbitrary subsets of a v. space v. 2. let x be an arbitrary vector such that x belongs to (s1 union s2). so x belongs to s1 or x belongs to s2. Let s1 and s2 be subsets of a vector space v. prove that span (s1∩s2)subespan (s1)∪span (s2). give an example in which span (s1∩s2) and span (s1)∩span (s2) are equal and one in which they are unequal. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.

Solved 2 Let S And S2 Be Subsets Of A Vector Space V Prove Chegg
