
Solved Chegg Chegg Chegg Chegg Chegg Chegg Chegg Chegg Chegg Chegg Prove the following identities using the standard identities shared in the lectures. start with one of the sides of the identity and arrive at the other side. 1. (1 cosx) (1−cosx)=sin2x 2. (tan2x)⋅ (1−cosx1 1 cosx1)=cos2x2 hint: work on the left hand side of the identity, by adding 1−cosx1 1 cosx1. 3. 1 tan2xtan2x=sin2x. Question: 2. (a) prove the following using the standard set identities. for any sets a, b and c: (a b c = a (buc) (b) is the following statement true for all sets a and b? p(a) up(b) sp(aub). if it is, give a proof and, if not, provide a counterexample, (recall that p(x) denotes the power set of x.).

Solved 2 Prove The Following Identities Using The Standard Chegg Use the set identities given in lecture 2 (pp, 22) to prove the following new identities label each step in your proof with the set identity used to establish that step. for example: a ∩ b = a ∪ b = a ∪ b . Free online trigonometric identity calculator verify trigonometric identities step by step. Using identity theorem, we can give proof of the standard trigonometric identities; in particular, $\sin^2 z \cos^2 z =1$. my approach: let $f(z) = \sin^2 z \cos^2 z 1$ , so $f$ is an entire function. Use the appropriate half angle identity to find the exact value of ⎜ ⎟ ⎝ 8 ⎠ use identities to find all solutions in the interval ⎡⎣ 0,2π ) . use identities to find the general solution, i.e., all solutions, to the following. in triangle efg, e = 4.56, e = 43o, and g = 57o. solve the triangle. in triangle abc, b = 24, b = 38o, and c = 21o.
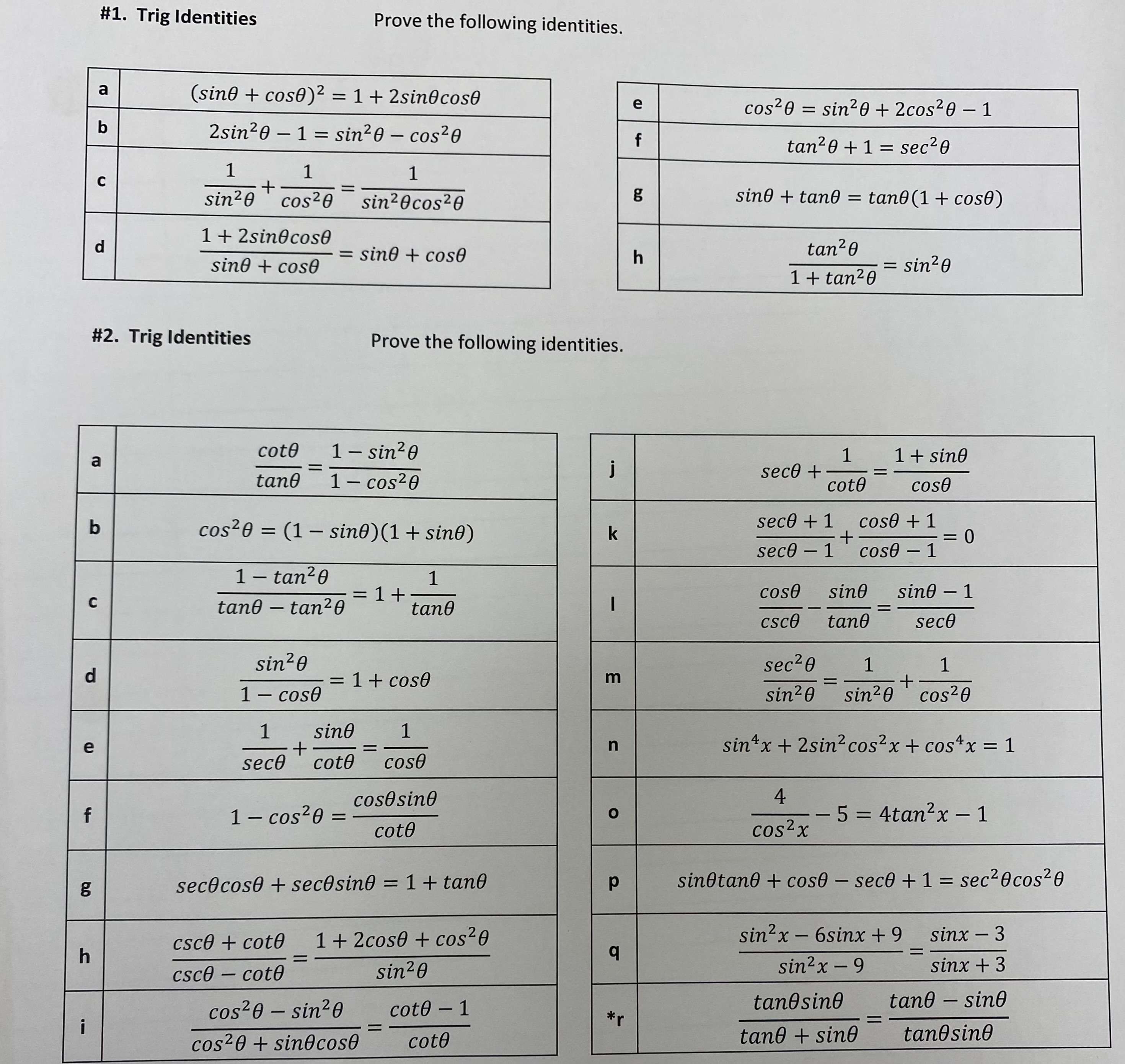
Solved 1 Trig Identities Prove The Following Identities Chegg Using identity theorem, we can give proof of the standard trigonometric identities; in particular, $\sin^2 z \cos^2 z =1$. my approach: let $f(z) = \sin^2 z \cos^2 z 1$ , so $f$ is an entire function. Use the appropriate half angle identity to find the exact value of ⎜ ⎟ ⎝ 8 ⎠ use identities to find all solutions in the interval ⎡⎣ 0,2π ) . use identities to find the general solution, i.e., all solutions, to the following. in triangle efg, e = 4.56, e = 43o, and g = 57o. solve the triangle. in triangle abc, b = 24, b = 38o, and c = 21o. Let $f$, $g$ and $h$ be any $c^{2}$ scalar functions. using the standard identities of vector calculus, prove that; $$ \nabla \cdot \left( f\nabla g \times \nabla h \right) = \nabla f \cdot \left(. Here is the list of the fundamental trigonometric identities and the types we use to verify them. now, let us verify a few such identities. verify: 1 tan2 θ = sec2 θ. step 1: using pythagorean identity. first, we start by identifying the identity which is needed. here, we will use the pythagorean identity: sin 2 θ cos 2 θ = 1. Ex 8.3, 4 prove the following identities, where the angles involved are acute angles for which the expressions are defined. (i) (cosec θ – cot θ)2 = (1 − 𝑐𝑜𝑠" " θ) (1 cosθ ) solving l.h.s (cosec θ – cot θ)2 we need to make it in terms of cos θ & sin θ = (1 sin𝜃 − cos𝜃 sin𝜃 )^2 =. Prove the identity: tan x cot x = sec x csc x. solution we begin by deciding whether to start with the expression on the right or the left. it is usually best to start with the more complicated expression, as it is eas ier to proceed from the complex toward the simple than to go in the other direction.

Solved Prove The Following Identities Using The Trig Chegg Let $f$, $g$ and $h$ be any $c^{2}$ scalar functions. using the standard identities of vector calculus, prove that; $$ \nabla \cdot \left( f\nabla g \times \nabla h \right) = \nabla f \cdot \left(. Here is the list of the fundamental trigonometric identities and the types we use to verify them. now, let us verify a few such identities. verify: 1 tan2 θ = sec2 θ. step 1: using pythagorean identity. first, we start by identifying the identity which is needed. here, we will use the pythagorean identity: sin 2 θ cos 2 θ = 1. Ex 8.3, 4 prove the following identities, where the angles involved are acute angles for which the expressions are defined. (i) (cosec θ – cot θ)2 = (1 − 𝑐𝑜𝑠" " θ) (1 cosθ ) solving l.h.s (cosec θ – cot θ)2 we need to make it in terms of cos θ & sin θ = (1 sin𝜃 − cos𝜃 sin𝜃 )^2 =. Prove the identity: tan x cot x = sec x csc x. solution we begin by deciding whether to start with the expression on the right or the left. it is usually best to start with the more complicated expression, as it is eas ier to proceed from the complex toward the simple than to go in the other direction.
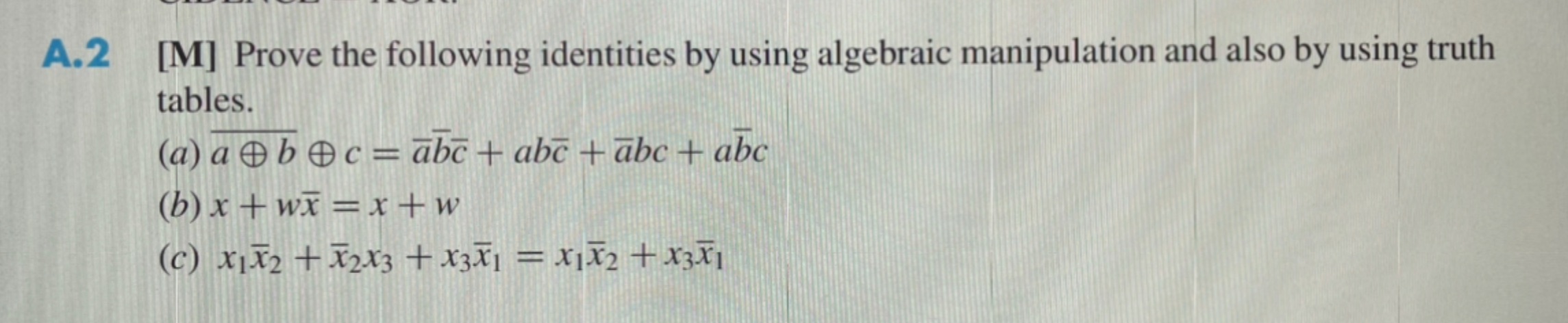
Solved Prove The Following Identities By Using Algebraic Chegg Ex 8.3, 4 prove the following identities, where the angles involved are acute angles for which the expressions are defined. (i) (cosec θ – cot θ)2 = (1 − 𝑐𝑜𝑠" " θ) (1 cosθ ) solving l.h.s (cosec θ – cot θ)2 we need to make it in terms of cos θ & sin θ = (1 sin𝜃 − cos𝜃 sin𝜃 )^2 =. Prove the identity: tan x cot x = sec x csc x. solution we begin by deciding whether to start with the expression on the right or the left. it is usually best to start with the more complicated expression, as it is eas ier to proceed from the complex toward the simple than to go in the other direction.
