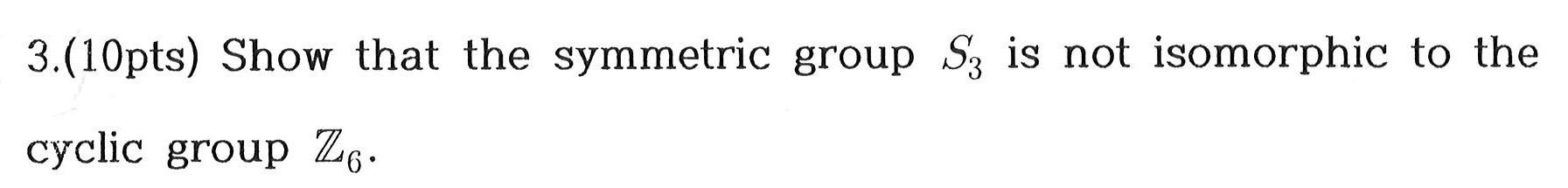
Solved 3 10pts Show That The Symmetric Group S3 Is Not Chegg There’s just one step to solve this. now as z 6 3. (10pts) show that the symmetric group s3 is not isomorphic to the cyclic group z6. Exercise 3.2 (a) show that the symmetric group s3 is non abelian, by finding two of its elements which do not commute. (b) show that sn is non abelian for any n≥3. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.
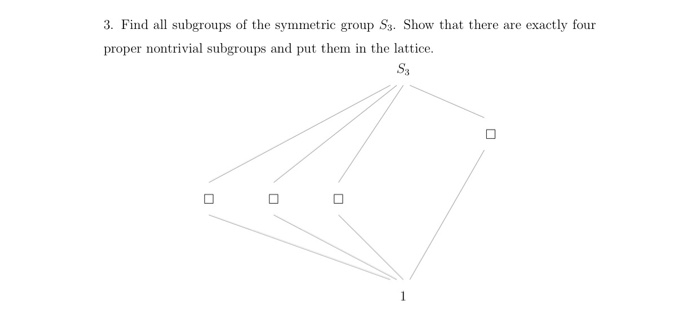
Solved 3 Find All Subgroups Of The Symmetric Group S3 Show Chegg Show that the elements of s3, the symmetric group of permutations of degree 3, are (a, aa, b, ba, baa, e) where a = (123), b = (12). show that is a normal subgroup of s3 but that is not. b. let h be a subgroup of g. show that for geg, g lhg is also a subgroup. Using the ad hoc approach presented in fulton and harris, compute the decompositions into direct sums of irreducible representation of the following representations of s3 s 3. for all of the problems, i am taking τ = (123) τ = (123) and σ = (12) σ = (12). This video consists on detail information of a symmetry group s3, how to make it by using symmetries and how to complete its cayley's table.at the end of the. The group s3, also known as the symmetric group on three letters, is not abelian. the order of the elements matters when performing the group operation. to determine if a group is abelian, we need to check if the group's operation is commutative.

Solved Consider The Symmetric Group S3 A ï By Identifying A Chegg This video consists on detail information of a symmetry group s3, how to make it by using symmetries and how to complete its cayley's table.at the end of the. The group s3, also known as the symmetric group on three letters, is not abelian. the order of the elements matters when performing the group operation. to determine if a group is abelian, we need to check if the group's operation is commutative. Multiplication on s 3 is functional compostion. so if f is in s 3, you want to answer the following question: "what is the smallest postive integer n, for which f°f° °f(x) = f n (x) = x, for all x in a?". Here’s the best way to solve it. to start showing that s 3 is indecomposable by proving that any direct product of subgroups of order 2 must be cyclic, first note that the order of any subgroup must divide the order of s 3. This example is of the symmetric group on 3 letters, usually denoted by s 3. here, we are considering the set of bijective functions on the set a = {1, 2, 3} which naturally arise as the set of permutations on a. our binary operation is function composition which results in a new bijective function. this example develops the table for s 3. we. Solution for the group s3 . let s3 be the symmetric group on 3 elements.(a) show that there are three conjugacy classes.(b) there are two characters of dimension 1, on s3 a3 .(c) let di.
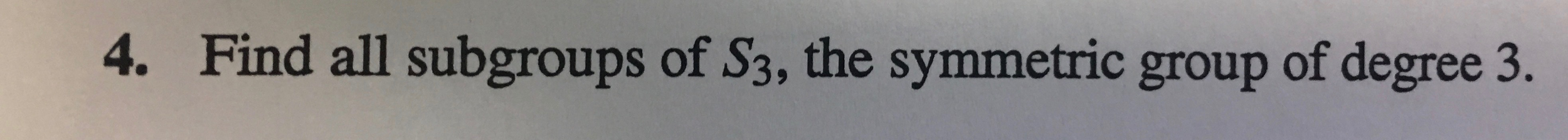
Solved Find All Subgroups Of S3 The Symmetric Group Chegg Multiplication on s 3 is functional compostion. so if f is in s 3, you want to answer the following question: "what is the smallest postive integer n, for which f°f° °f(x) = f n (x) = x, for all x in a?". Here’s the best way to solve it. to start showing that s 3 is indecomposable by proving that any direct product of subgroups of order 2 must be cyclic, first note that the order of any subgroup must divide the order of s 3. This example is of the symmetric group on 3 letters, usually denoted by s 3. here, we are considering the set of bijective functions on the set a = {1, 2, 3} which naturally arise as the set of permutations on a. our binary operation is function composition which results in a new bijective function. this example develops the table for s 3. we. Solution for the group s3 . let s3 be the symmetric group on 3 elements.(a) show that there are three conjugacy classes.(b) there are two characters of dimension 1, on s3 a3 .(c) let di.
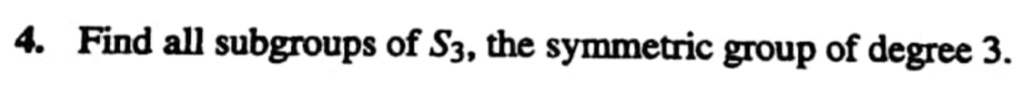
Solved 4 Find All Subgroups Of S3 The Symmetric Group Of Chegg This example is of the symmetric group on 3 letters, usually denoted by s 3. here, we are considering the set of bijective functions on the set a = {1, 2, 3} which naturally arise as the set of permutations on a. our binary operation is function composition which results in a new bijective function. this example develops the table for s 3. we. Solution for the group s3 . let s3 be the symmetric group on 3 elements.(a) show that there are three conjugacy classes.(b) there are two characters of dimension 1, on s3 a3 .(c) let di.
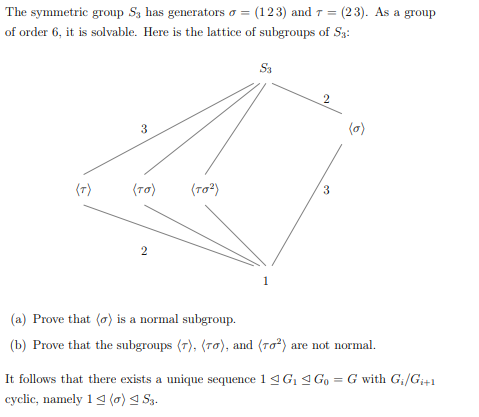
Solved The Symmetric Group S3 Has Generators σ 123 And Chegg
