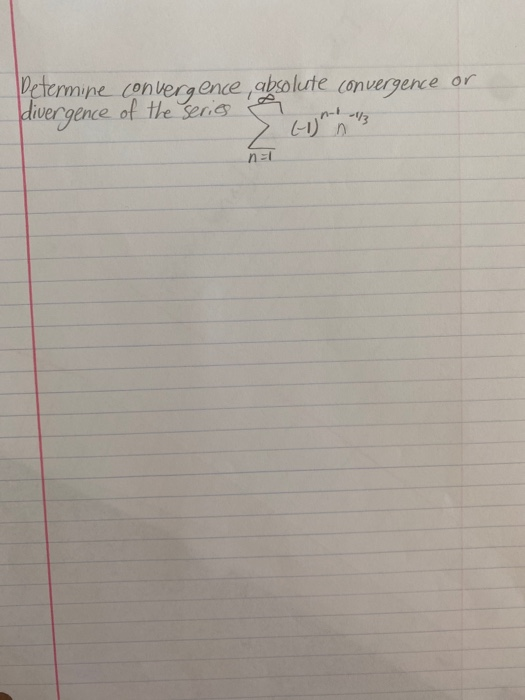
Solved Determine Convergence Absolute Convergence Or Chegg To determine the convergence of each series, we'll use the root test and ratio test. let's start wit. For each of the following series determine if they are absolutely convergent, conditionally convergent or divergent. \( \displaystyle \sum\limits {n = 2}^\infty {\frac{{{{\left( { 1} \right)}^{n 1}}}}{{{n^3} 1}}} \) solution.
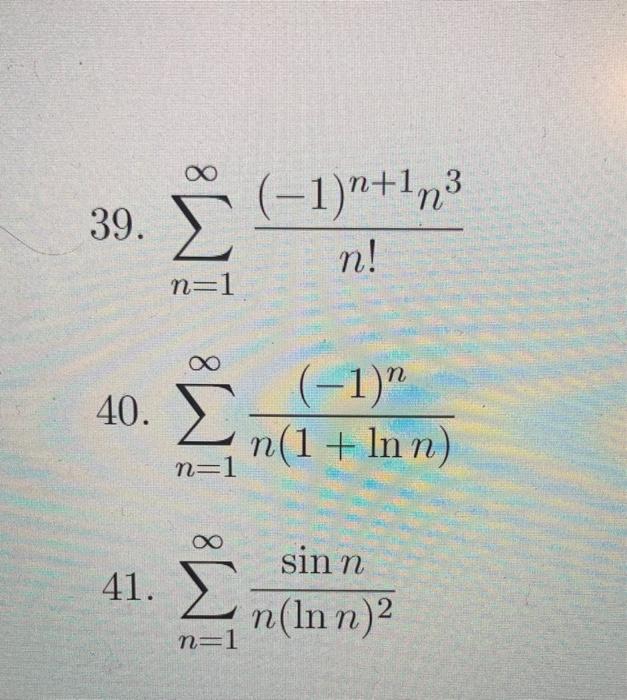
Solved Determine Either Absolute Convergence Conditional Chegg Determine if the series converges absolutely, converges conditionally, or diverges. find the exact value for the sum of the convergent series. $$1 \frac{1}{5} \frac{1}{5^2} \frac{1}{5^3} \frac{1}{5^4} \frac{1}{5^5} \frac{1}{5^6} \frac{1}{5^7} \frac{1}{5^8} $$ i have no clue where to start. In each case determine whether the given series is absolutely convergent, conditionally convergent, or diverges. name any convergence test(s) you use, and justify all of your work. For each series, determine what information, if any, the root or ratio test gives. show the details of your limit computation. a) ( ) = − 2 0 1 1 n n n conclusion: b) = 1 3 n n n e n conclusion: c) = 0 !. Free online series convergence calculator check convergence of infinite series step by step.
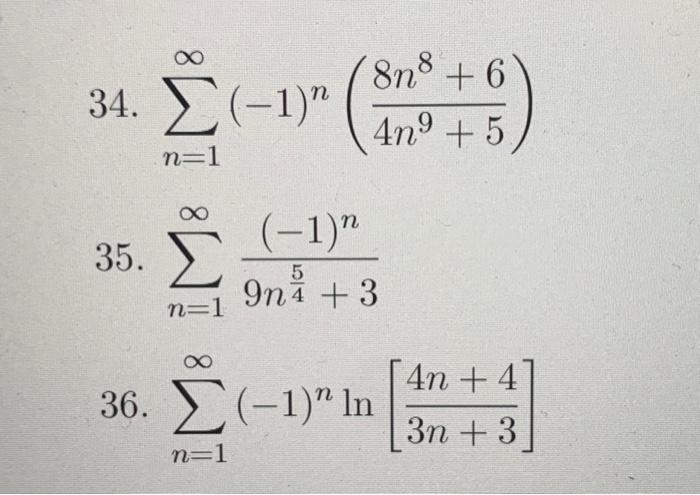
Solved Determine Either Absolute Convergence Conditional Chegg For each series, determine what information, if any, the root or ratio test gives. show the details of your limit computation. a) ( ) = − 2 0 1 1 n n n conclusion: b) = 1 3 n n n e n conclusion: c) = 0 !. Free online series convergence calculator check convergence of infinite series step by step. For each of the following series, determine which convergence test is the best to use and explain why. then determine if the series converges or diverges. if the series is an alternating series, determine whether it converges absolutely, converges conditionally, or diverges. ∞ ∑ n=1 (−1)n 1(3n 1) n! ∑ n = 1 ∞ (− 1) n 1 (3 n 1) n!. Let the series $\sum {n=0}^\infty{\frac{a n}{3^n}}$ be convergent, but the series $\sum {n=0}^\infty{\frac{{( 1)^n}{a n}}{3^n}} $ be divergent. show whether: a)$\sum {n=0}^\infty{\frac{a n}{3^n}}$ is absolutely convergent or conditionally convergent. Example 1 determine if each of the following series are absolute convergent, conditionally convergent or divergent. \(\displaystyle \sum\limits {n = 1}^\infty {\frac{{{{\left( { 1} \right)}^n}}}{n}} \). In this maths article we will look into the absolute convergence definition, test, series and solved examples in detail. if the series ∑nun ∑ n u n converges, with ∑n|un| ∑ n | u n | signifying the absolute value, then the series |un| | u n | is said to converge absolutely.

Solved Determine Either Absolute Convergence Conditional Chegg For each of the following series, determine which convergence test is the best to use and explain why. then determine if the series converges or diverges. if the series is an alternating series, determine whether it converges absolutely, converges conditionally, or diverges. ∞ ∑ n=1 (−1)n 1(3n 1) n! ∑ n = 1 ∞ (− 1) n 1 (3 n 1) n!. Let the series $\sum {n=0}^\infty{\frac{a n}{3^n}}$ be convergent, but the series $\sum {n=0}^\infty{\frac{{( 1)^n}{a n}}{3^n}} $ be divergent. show whether: a)$\sum {n=0}^\infty{\frac{a n}{3^n}}$ is absolutely convergent or conditionally convergent. Example 1 determine if each of the following series are absolute convergent, conditionally convergent or divergent. \(\displaystyle \sum\limits {n = 1}^\infty {\frac{{{{\left( { 1} \right)}^n}}}{n}} \). In this maths article we will look into the absolute convergence definition, test, series and solved examples in detail. if the series ∑nun ∑ n u n converges, with ∑n|un| ∑ n | u n | signifying the absolute value, then the series |un| | u n | is said to converge absolutely.

Solved Given The Following Series Determine Absolute Chegg Example 1 determine if each of the following series are absolute convergent, conditionally convergent or divergent. \(\displaystyle \sum\limits {n = 1}^\infty {\frac{{{{\left( { 1} \right)}^n}}}{n}} \). In this maths article we will look into the absolute convergence definition, test, series and solved examples in detail. if the series ∑nun ∑ n u n converges, with ∑n|un| ∑ n | u n | signifying the absolute value, then the series |un| | u n | is said to converge absolutely.
