
Solved 3 Analyze The Series σ001 An For Absolute And Chegg Analyze the series Σ 1 an for absolute and conditional convergence. rn your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Using sup inf’s and the absolute value. the definition of sequences of real numbers and convergence of sequences. subsequences. the relations between limits and order, algebraic operations and the absolute value on the set of real numbers. the bolzano weierstrass theorem.

Solved Analyze The Series For Absolute And Conditional Chegg 3. basic properties proposition 3.1 (alternating series test). let (a n) be a decreasing sequence of non negative real numbers. then the series x∞ j=1 (−1)ja j (3.1) is convergent if and only if the sequence a n converges to 0. proposition 3.2. suppose that the series x∞ j=m a j and x∞ j=m b j (3.2) are convergent, then, ∀c,d ∈r the. Theorem 1. (alternating series test) consider the series. n. ∞ (−1) j. a. j, j=0. where a. j > 0. if (a. j) converges to zero (as a sequence), then the series is convergent. the main problem with conditionally convergent series is that if the terms are rearranged, then the series may converge to a different limit. the “safe. Verify the associative law for multiplication of complex numbers. that is, show that. proof. let zk = xk iyk for k = 1;2;3. then. 5. compute. (1 2i)4. 7 24i. 6. let f be the map sending each complex number. = x yi! proof. let zk = xk yki for k = 1;2. then. therefore, f (z1z2) = f (z1) f (z2). 7. use binomial theorem. To analysis: series robert c. vaughan series tests for convergence of series proofs of the tests further theorems and examples power series •example 6.1. let x ∈r and a n = xn, so that s n = x x2 xn = x −xn 1 1 −x (x ̸= 1) . •by example 4.9, when |x|<1 we have lim n→∞xn = 0. •thus, in that case the series converges and.

Solved Analyze The Following Series For Absolute And Chegg Verify the associative law for multiplication of complex numbers. that is, show that. proof. let zk = xk iyk for k = 1;2;3. then. 5. compute. (1 2i)4. 7 24i. 6. let f be the map sending each complex number. = x yi! proof. let zk = xk yki for k = 1;2. then. therefore, f (z1z2) = f (z1) f (z2). 7. use binomial theorem. To analysis: series robert c. vaughan series tests for convergence of series proofs of the tests further theorems and examples power series •example 6.1. let x ∈r and a n = xn, so that s n = x x2 xn = x −xn 1 1 −x (x ̸= 1) . •by example 4.9, when |x|<1 we have lim n→∞xn = 0. •thus, in that case the series converges and. Determines convergence or divergence of an infinite series. calculates the sum of a convergent or finite series. 12.determine whether the following series converge absolutely, converge conditionally, or diverge. state the tests that you used and give a brief explanation. for example: for problem 11.6:13 you could write \converges absolutely by direct comparison test, since ja nj= jcos(nˇ=3)=n!j 1=n!, and p p 1=n! converges by the ratio test since. Give an example of divergent series Σ001 an and Ση bn for which the series n= Σ (an bn) converges. 1. for each of the following infinite series, decide whether the series converges or diverges and explain your answer. if the series is a convergent geometric series, find its sum. Prove that 12 22 ··· n2=1 6. n(n 1)(2n 1) for all n ∈ n. put f(n) = n(n 1)(2n 1) 6. then f(1) = 1, i.e the theorem holds true for n = 1. to prove the theorem, it suffices to assume that it holds true for n = m and derive it for n = m 1, m = 1,2,3, . we have f(m 1)− f(m) = 1 6 (m 1)[(2m 3)(m 2)− m(2m 1)] = 1 6 (m 1)(6m 6) = (m 1)2.
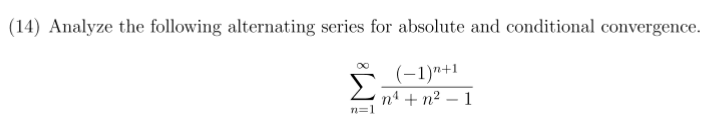
Solved 14 Analyze The Following Alternating Series For Chegg Determines convergence or divergence of an infinite series. calculates the sum of a convergent or finite series. 12.determine whether the following series converge absolutely, converge conditionally, or diverge. state the tests that you used and give a brief explanation. for example: for problem 11.6:13 you could write \converges absolutely by direct comparison test, since ja nj= jcos(nˇ=3)=n!j 1=n!, and p p 1=n! converges by the ratio test since. Give an example of divergent series Σ001 an and Ση bn for which the series n= Σ (an bn) converges. 1. for each of the following infinite series, decide whether the series converges or diverges and explain your answer. if the series is a convergent geometric series, find its sum. Prove that 12 22 ··· n2=1 6. n(n 1)(2n 1) for all n ∈ n. put f(n) = n(n 1)(2n 1) 6. then f(1) = 1, i.e the theorem holds true for n = 1. to prove the theorem, it suffices to assume that it holds true for n = m and derive it for n = m 1, m = 1,2,3, . we have f(m 1)− f(m) = 1 6 (m 1)[(2m 3)(m 2)− m(2m 1)] = 1 6 (m 1)(6m 6) = (m 1)2.
