Solved 3 Let 1 3 1 0 A 1 1 1 0 1 1 0 3 1 0 1 A 2 Chegg

Solved Let A 1 1 1 1 1 1 2 3 4 5 1 1 1 1 1 1 0 3 2 Chegg Question: 3. let 1 3 1 0 a= 1 1 1 0 1 1 0 3 1 0 1 (a) [2 marks] show that and are eigenvectors of a, where i is the imaginary unit i= 1. (b) [5 marks] solve the differential system y4 3y1 yi y ป) ys ya y2 y2 y2 y2 y3 3y3 94 ya yi = with initial conditions yı (0) = y2 (0) y3 (0) = y (0) = 1. show your workings clearly. Let vectors a = (1, 0, −3), b = (−2, 5, 1), and c = (3, 1, 1). calculate the following, expressing your answers as ordered triples (three comma separated numbers).

Solved Let A 1 1 2 3 A Let Chegg Let a = \ (\begin {pmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end {pmatrix}\) and b = 7a20 20a7 2i, where i is an identity matrix of order 3 × 3. if b = [bij], then b13 is equal to . Injective (recall injective means one to one)? why or why not? (1. points) since m has two free variables, it has two co. umns without pivots. since it has four columns, it must have only 2 pivots. therefore we note that m doesn't have a piv. Correct option is (b) infinitely many solutions. Ask yourself if the three form a linearly independent set using known techniques (e.g. row reducing). conclude that since you have three linearly independent vectors in a three dimensional space, they must span the whole space.

Solved Let A 1 1 2 1 3 0 1 1 0 1 1 2 0 1 3 4 0 1 0 2 1 Chegg Correct option is (b) infinitely many solutions. Ask yourself if the three form a linearly independent set using known techniques (e.g. row reducing). conclude that since you have three linearly independent vectors in a three dimensional space, they must span the whole space. Let vectors a = (1,0,−3), b = (−2,5,1), and c = (3,1,1). calculate the following, and express your answers as ordered triplets of values separated by commas. Let a be a 3 × 3 matrix such that a [ (1, 2, 3), (0, 2, 3), (0, 1, 1)] = [ (0, 0, 1), (1, 0, 0), (0, 1, 0)] then a 1 is. To solve the problem, we need to analyze the set s and the conditions for the matrices in t n. where a,b are integers from 1 to 100. where i is the identity matrix. we need to find the values of n such that an(n 1) = i. from b2 = 1, we find b= 1 (since b must be in {1,2,…,100}). this is always true for any a. However, the pair $ (1,1)$ is not going to be added as there exist no pairs where $1$ is the second entry (nothing leads to it). as such, it doesn't cause any problem for the transitivity of the relation.

Solved Let A 2 1 1 1 0 2 1 0 1 B 2 2 0 1 2 2 4 Chegg Let vectors a = (1,0,−3), b = (−2,5,1), and c = (3,1,1). calculate the following, and express your answers as ordered triplets of values separated by commas. Let a be a 3 × 3 matrix such that a [ (1, 2, 3), (0, 2, 3), (0, 1, 1)] = [ (0, 0, 1), (1, 0, 0), (0, 1, 0)] then a 1 is. To solve the problem, we need to analyze the set s and the conditions for the matrices in t n. where a,b are integers from 1 to 100. where i is the identity matrix. we need to find the values of n such that an(n 1) = i. from b2 = 1, we find b= 1 (since b must be in {1,2,…,100}). this is always true for any a. However, the pair $ (1,1)$ is not going to be added as there exist no pairs where $1$ is the second entry (nothing leads to it). as such, it doesn't cause any problem for the transitivity of the relation.
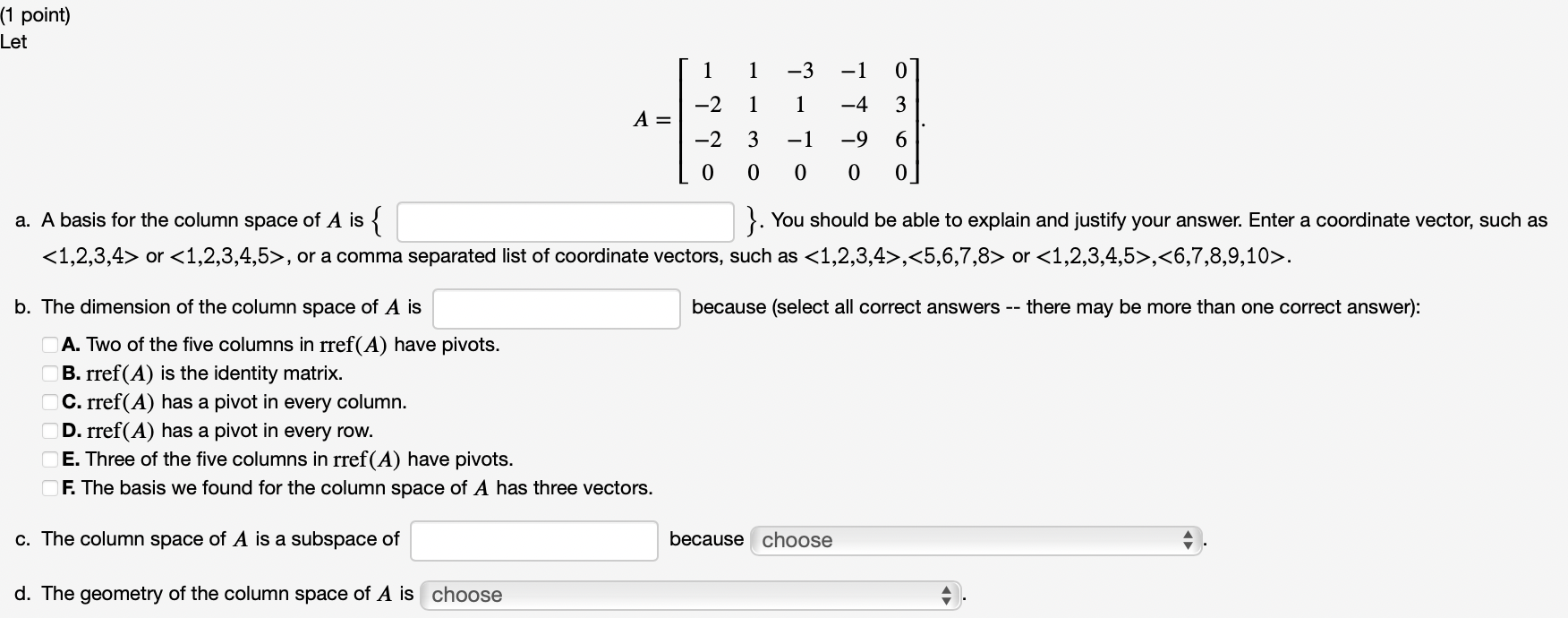
Solved 1 Point Let 1 1 3 1 0 2 1 1 4 3 A 2 3 1 6 9 Chegg To solve the problem, we need to analyze the set s and the conditions for the matrices in t n. where a,b are integers from 1 to 100. where i is the identity matrix. we need to find the values of n such that an(n 1) = i. from b2 = 1, we find b= 1 (since b must be in {1,2,…,100}). this is always true for any a. However, the pair $ (1,1)$ is not going to be added as there exist no pairs where $1$ is the second entry (nothing leads to it). as such, it doesn't cause any problem for the transitivity of the relation.
Comments are closed.