
Solved 26 Let R Be The Relation R A B в јa Chegg Let r be the relation { (1,2), (1,3), (2,3), (2,4), (3,1)}, and let s be the relation { (2,1), (3,1), (3,2), (4,2)}. find s∘r. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: 32. Question 32 (2 points) for the following problem, let r be the relation { (a,b), (a.c), (b,b), (c.c), (c), (d,b) over the set (a,b,c,d). which matrix is the symmetric closure of r?.
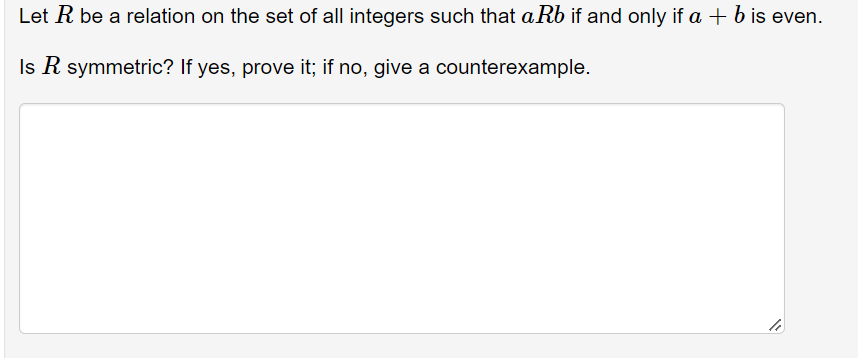
Solved Let R Be A Relation On The Set Of All Integers Such Chegg We will be using the definitions of reflexive relation, symmetric relations and transitive relations to verify if each relation holds or not and hence deduce the answer. complete step by step solution. Let r (abcdefgh) be a relation schema and f be the set of dependencies f = {a → b, abcd → e, ef → g, ef → h and acdf →eg}. the minimal cover of a set of functional dependencies is. correct answer is option1. explanation: use the union rule to replace. ef → g and ef → h. ef → gh. f = { a → b abcd → e ef → gh acdf → eg }. Let r be the relation {(1,2),(1,3),(2,3),(2,4),(3,1)}, and let s be the relation {(2,1),(3,1),(3,2),(4,2)}. find s∘r.2. which 4 tuples are in the relation {(a,b,c,d)∣a,b,c, and d are positive integers with abcd=6} ?. The relation r is defined as arb if and only if a divides b. this means that if we can divide b by a without any remainder, then the ordered pair (a, b) belongs to the relation r. let's evaluate each of the given options: option a. (2,4), (3,6) (2,4): 4 divided by 2 equals 2 with no remainder, so (2,4) belongs to r.

Solved 3 Let S Be A Set And Let R Be A Relation On S Which Chegg Let r be the relation {(1,2),(1,3),(2,3),(2,4),(3,1)}, and let s be the relation {(2,1),(3,1),(3,2),(4,2)}. find s∘r.2. which 4 tuples are in the relation {(a,b,c,d)∣a,b,c, and d are positive integers with abcd=6} ?. The relation r is defined as arb if and only if a divides b. this means that if we can divide b by a without any remainder, then the ordered pair (a, b) belongs to the relation r. let's evaluate each of the given options: option a. (2,4), (3,6) (2,4): 4 divided by 2 equals 2 with no remainder, so (2,4) belongs to r. Let r r be a relation on \mathbb {q} q such that \dfrac {p} {q}\,r\,\dfrac {s} {t}\! qp r ts. (i) since pq = qp\! pq = qp, \dfrac {p} {q}\,r\,\dfrac {p} {q}\! qp r qp. therefore, r r is reflexive. (ii) suppose that \dfrac {p} {q}\,r\,\dfrac {s} {t}\! qp r ts. then, pt = qs\! pt = qs. The relation r defined by sets having the same cardinality is shown to be an equivalence relation as it is reflexive, symmetric, and transitive. the equivalence class of the set {0, 1, 2} includes all sets with three elements, and the equivalence class of \mathbb{z}\ includes all countably infinite sets. If l is the set of integers and if the relation r is defined over l by arb, iff a b is an even integer, `a,b inl`, the relation r is. R is the relation defined on the set of integers by xry when ⌊x 2⌋ = ⌊y 2⌋. prove that r is an equivalence relation and find the equivalence classes.

Solved 2 Let R Be Relation Defined By Chegg Let r r be a relation on \mathbb {q} q such that \dfrac {p} {q}\,r\,\dfrac {s} {t}\! qp r ts. (i) since pq = qp\! pq = qp, \dfrac {p} {q}\,r\,\dfrac {p} {q}\! qp r qp. therefore, r r is reflexive. (ii) suppose that \dfrac {p} {q}\,r\,\dfrac {s} {t}\! qp r ts. then, pt = qs\! pt = qs. The relation r defined by sets having the same cardinality is shown to be an equivalence relation as it is reflexive, symmetric, and transitive. the equivalence class of the set {0, 1, 2} includes all sets with three elements, and the equivalence class of \mathbb{z}\ includes all countably infinite sets. If l is the set of integers and if the relation r is defined over l by arb, iff a b is an even integer, `a,b inl`, the relation r is. R is the relation defined on the set of integers by xry when ⌊x 2⌋ = ⌊y 2⌋. prove that r is an equivalence relation and find the equivalence classes.

Solved 2 Let A 1 2 3 4 Let R Be The Relation On A Chegg If l is the set of integers and if the relation r is defined over l by arb, iff a b is an even integer, `a,b inl`, the relation r is. R is the relation defined on the set of integers by xry when ⌊x 2⌋ = ⌊y 2⌋. prove that r is an equivalence relation and find the equivalence classes.
