Solved 4 5 Derivatives And Shapes Of Graphs Problem 6 4 Chegg

Solved 4 5 Derivatives And Shapes Of Graphs Problem 6 4 Chegg Question: 4.5 derivatives and shapes of graphs: problem 6 (4 points) below is the graph of the derivative f′ (x) of a function defined on the interval (0,8). you can click on the graph to see a larger version in a separate window. Therefore, to test whether a function has a local extremum at a critical point c c, we must determine the sign of f′(x) f ′ (x) to the left and right of c c. this result is known as the first derivative test.

Solved 4 5 Derivatives And Shapes Of Graphs Problem 8 1 Chegg For the following exercises (8 12), analyze the graphs of [latex]f^ {\prime} [ latex], then list all intervals where [latex]f [ latex] is increasing or decreasing. We analyze the concavity of a given function by using a similar strategy that we used when analyzing intervals of increasing and decreasing values. only this time, because we are talking about. We have now developed the tools we need to determine where a function is increasing and decreasing, as well as acquired an understanding of the basic shape of the graph. If f(x) is concave up on an interval, then the graph of f(x) will lie above the tangent lines on the interval. (graph bends upwards.) if f00(c) < 0, we say that f(x) is concave down at c. if f(x) is concave down on an interval, then the graph of f(x) will lie below the tangent lines on the interval. (graph bends downwards.).

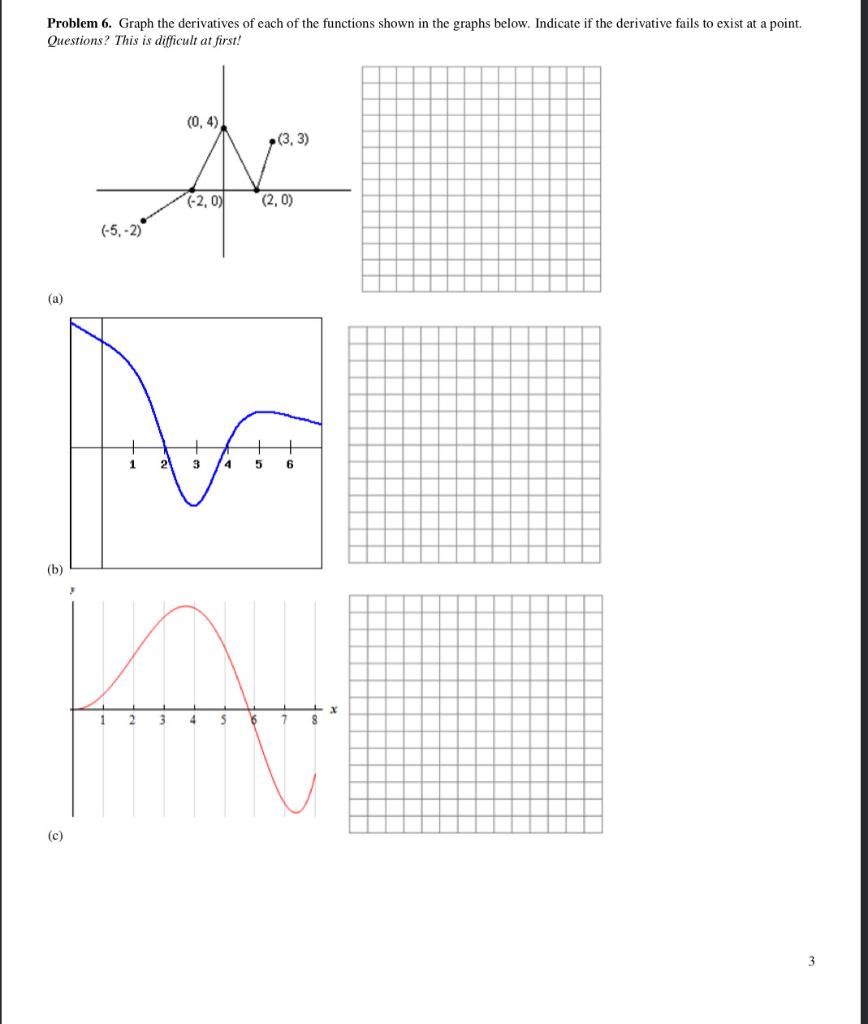
Solved Problem 6 Graph The Derivatives Of Each Of The Chegg We have now developed the tools we need to determine where a function is increasing and decreasing, as well as acquired an understanding of the basic shape of the graph. If f(x) is concave up on an interval, then the graph of f(x) will lie above the tangent lines on the interval. (graph bends upwards.) if f00(c) < 0, we say that f(x) is concave down at c. if f(x) is concave down on an interval, then the graph of f(x) will lie below the tangent lines on the interval. (graph bends downwards.). Study with quizlet and memorize flashcards containing terms like increasing and decreasing (i d test), graphing f (x) using f' (x) and f'' (x), first derivative test (fdt) and more. Question: 4.5 derivatives and shapes of graphs: (8 points) please answer the following questions about the function f (x)=6x5−6x4. instructions: if you are asked to find x or y values, enter either a number, a list of numbers separated by commas, or none if there aren't any solutions. 4.5 derivatives and the shape of a graph ryan melton 1.43k subscribers subscribed. In the following table, we evaluate the second derivative at each of the critical points and use the second derivative test to determine whether f has a local maximum or local minimum at any of these points.