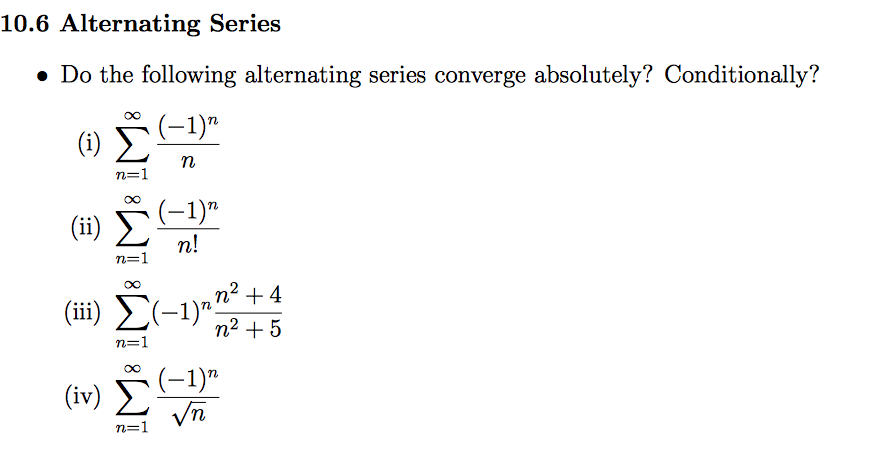
Solved Alternating Series Do The Following Alternating Chegg To determine how many terms you need to compute for the approximation to be within from the convergent value, first identify the general term of the alternating series and use the approximation condition:. Our expert help has broken down your problem into an easy to learn solution you can count on. question: (5 points) for the following alternating series, 066) (0.05 0.6 3! 5! 7! n how many terms do you have to compute in order for your approximation (your partial sum) to be within 0.0000001 from the convergent value of that series?.

Solved 5 Points For The Following Alternating Series Chegg An alternating series is a series whose terms alternate in sign, i.e., \sum {n=0}^\infty ( 1)^na n = a 0 a 1 a 2 a 3 ··· ∑n=0∞ (−1)nan = a0 − a1 a2 − a3 ⋅⋅⋅ where either all a n are positive or all a n are negative. theorem. alternating series test. it states that an alternating series converges if the following two conditions are met:. Video answer: in this problem we are given the alternating series given by summation. from an equal to one to infinity of a n. equal to 0.5 minus 0.5 q divided by three factorial plus 0.5 raised to the power five divided by five factorial minus 0.5. For each of the following series, determine (with proof) if it converges absolutely, converges conditionally, or diverges. solution. and the series diverges to ∞ by comparison with the harmonic series. then (an) is a decreasing sequences with an 0 as n → so the alternating series test implies that the series con verges. Answer to (5 points) for the following alternating series,.
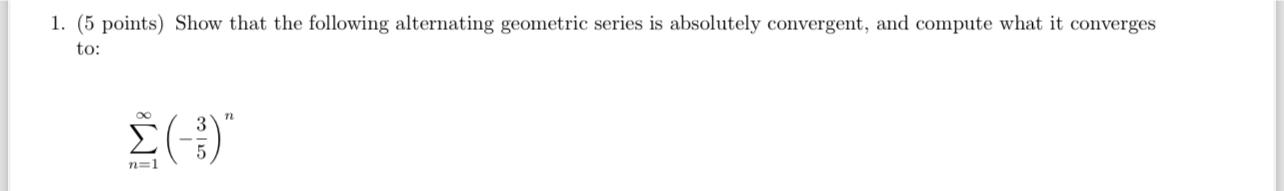
Solved 5 ï Points ï Show That The Following Alternating Chegg For each of the following series, determine (with proof) if it converges absolutely, converges conditionally, or diverges. solution. and the series diverges to ∞ by comparison with the harmonic series. then (an) is a decreasing sequences with an 0 as n → so the alternating series test implies that the series con verges. Answer to (5 points) for the following alternating series,. 1 to fill in the table below. plot the points , on the graph. if you have an alternating series that converges, we can approximate the sum of the series! write your questions and thoughts here! determine the number of terms required to approximate the sum of the series with an error less than 10 . Test the series for convergence or divergence using the alternating series test. identify b n. (assume the series starts at n = 1.) evaluate the following limit. there are 2 steps to solve this one. 1 ln (4) − 1 ln (5) 1 ln (6) − 1 ln (7) 1 ln (8) − … we can identify bn as the absolute value of the terms of the series, which i. Example 1 test the following series for convergence x1 n=1 ( 1)n 1 n i we have b n = 1 n. i lim n!1 1 n = 0. i b n 1 = 1 n 1 < n = 1 n for all n 1. i therefore, we can conclude that the alternating series p 1 n=1 ( 1) n 1 converges. i note that an alternating series may converge whilst the sum of the absolute values diverges. in particular the. Alternating series test if the terms ? 𝑛 of an alternating series, satisfy the following three conditions: •? 𝑛 > 0 (thus all the terms alternate in sign either from positive to negative for all n or from negative to positive for all n), • lim 𝑛→∞ ? 𝑛 = 0 (thus the terms of the series ? 𝑛 form a null sequence), • the.

Solved Alternating Series Prove That The Following Series Chegg 1 to fill in the table below. plot the points , on the graph. if you have an alternating series that converges, we can approximate the sum of the series! write your questions and thoughts here! determine the number of terms required to approximate the sum of the series with an error less than 10 . Test the series for convergence or divergence using the alternating series test. identify b n. (assume the series starts at n = 1.) evaluate the following limit. there are 2 steps to solve this one. 1 ln (4) − 1 ln (5) 1 ln (6) − 1 ln (7) 1 ln (8) − … we can identify bn as the absolute value of the terms of the series, which i. Example 1 test the following series for convergence x1 n=1 ( 1)n 1 n i we have b n = 1 n. i lim n!1 1 n = 0. i b n 1 = 1 n 1 < n = 1 n for all n 1. i therefore, we can conclude that the alternating series p 1 n=1 ( 1) n 1 converges. i note that an alternating series may converge whilst the sum of the absolute values diverges. in particular the. Alternating series test if the terms ? 𝑛 of an alternating series, satisfy the following three conditions: •? 𝑛 > 0 (thus all the terms alternate in sign either from positive to negative for all n or from negative to positive for all n), • lim 𝑛→∞ ? 𝑛 = 0 (thus the terms of the series ? 𝑛 form a null sequence), • the.

Solved Question 2 15 Points Consider The Following Chegg Example 1 test the following series for convergence x1 n=1 ( 1)n 1 n i we have b n = 1 n. i lim n!1 1 n = 0. i b n 1 = 1 n 1 < n = 1 n for all n 1. i therefore, we can conclude that the alternating series p 1 n=1 ( 1) n 1 converges. i note that an alternating series may converge whilst the sum of the absolute values diverges. in particular the. Alternating series test if the terms ? 𝑛 of an alternating series, satisfy the following three conditions: •? 𝑛 > 0 (thus all the terms alternate in sign either from positive to negative for all n or from negative to positive for all n), • lim 𝑛→∞ ? 𝑛 = 0 (thus the terms of the series ? 𝑛 form a null sequence), • the.
