
Solved 5 Show That The Two Lines в 1 3 2 в 1 S 1 6 1 And Chegg Show that the two lines ℓ1:(3,2,−1) s(1,6,1) and ℓ2:(1,0,1) t(1,−3,−4)s,t∈r do not intersect in r3. (be careful; in r3, non parallel lines may not intersect.) your solution’s ready to go!. Let a be a fixed point on l 1 eg 3, 2, 1 and let b be a general point on l 2 2 μ, μ, 4 μ. attempt to find vector ab → (m1) ab → = 1 2 5 μ 1 1 1 μ ∈ ℝ a1. ab → = 1 μ 2 2 μ 2 5 μ 2 = 3 μ 2 12 μ 30 m1. either. null a1. or. ab → = 3 μ 2 2 18 to obtain μ = 2 a1. then.
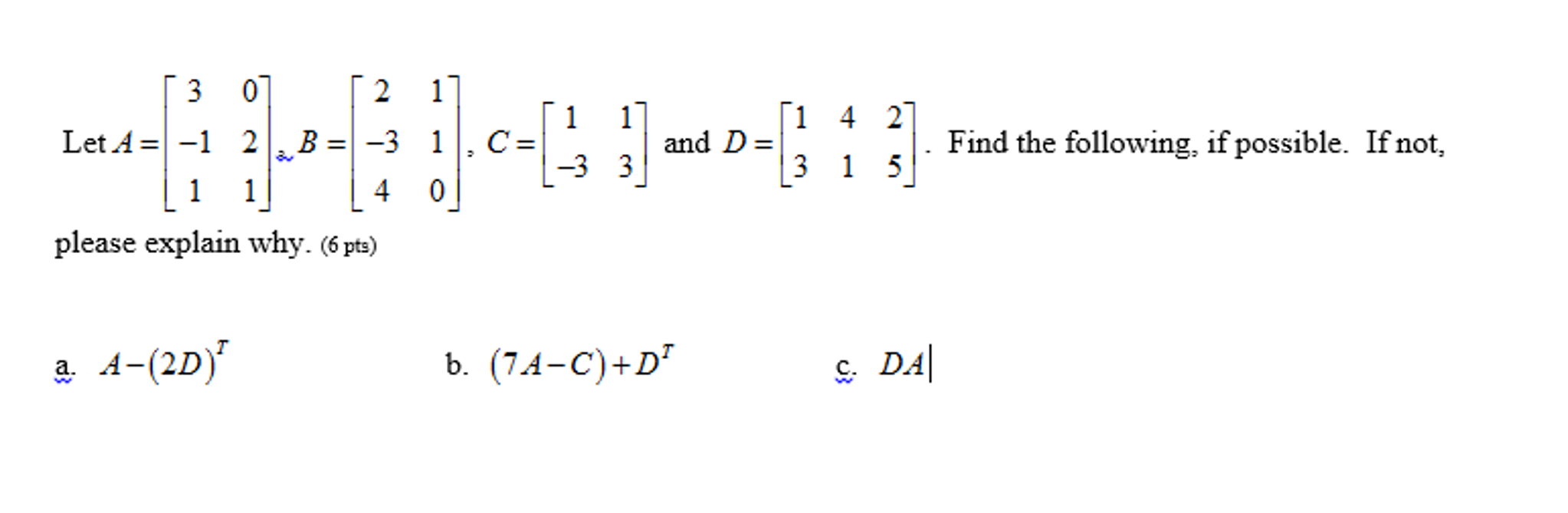
Solved Let A 3 0 1 2 1 1 B 2 1 3 1 4 0 C Chegg Hx 2;y 1;z 1ih1; 3;2i= 0 that is (x 2) 3(y 1) 2(z 1) = 0; so that rearranging we have x 3y 2z = 3. pick any point of the rst line. if we set t = 0 we get r = ( 4;1; 2). the line through r parallel to ~n intersects the plane at the closest point r0to r. this line is ~r(t) = h 4;1; 2i th1; 3;2i= h 4 t;1 3t; 2 2ti: this lies on the plane when. Free math problem solver answers your algebra homework questions with step by step explanations. So what you want to see is if there exists realy numbers $t,s$ such that $$ (3,4,1) t (2, 1,3) = (1,3,4) s(4, 2,5), $$ i.e. find $s$ and $t$ such that the point can be on both lines. We have shown that the given lines satisfy both of the necessary conditions to be classified as skew. the lines are therefore skew, as required. recall that for two lines to be skew they must satisfy two conditions: 1) they must not be parallel. 2) they must not intersect.
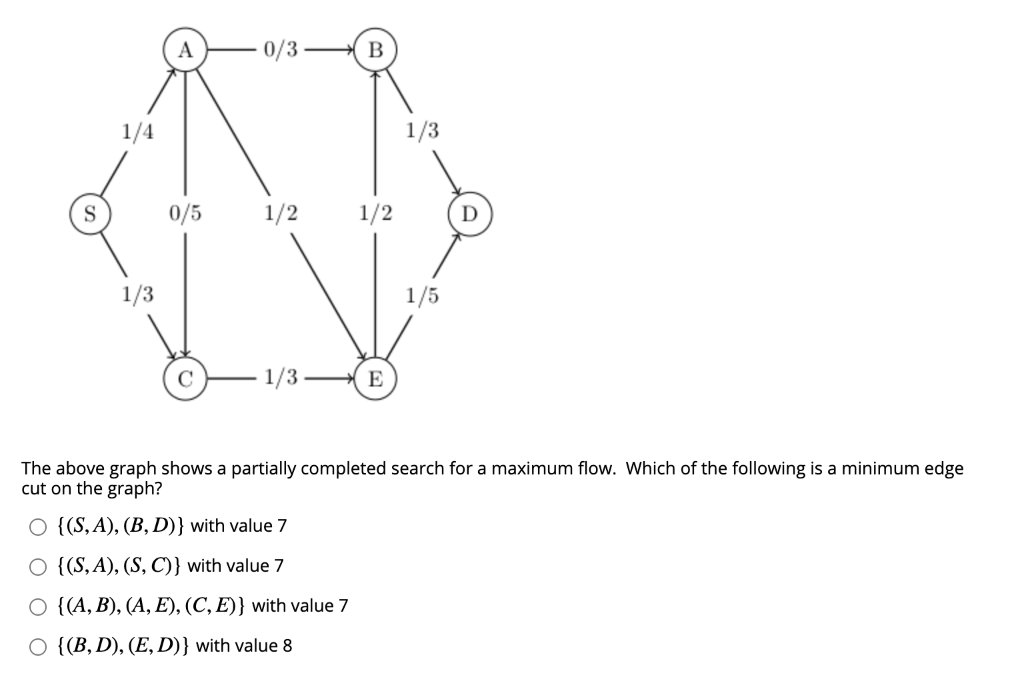
Solved 0 3 B 1 4 1 3 S 0 5 1 2 1 2 D 1 3 1 5 с 1 3 E The Chegg So what you want to see is if there exists realy numbers $t,s$ such that $$ (3,4,1) t (2, 1,3) = (1,3,4) s(4, 2,5), $$ i.e. find $s$ and $t$ such that the point can be on both lines. We have shown that the given lines satisfy both of the necessary conditions to be classified as skew. the lines are therefore skew, as required. recall that for two lines to be skew they must satisfy two conditions: 1) they must not be parallel. 2) they must not intersect. H1,2,3i (the direction vectors of the two lines). so set ~n = h1,1,1i×h1,2,3i = h3− 2,−3 1,2−1i = h1,−2,1i. from above, we have found that (0,0,0) and (−1,0,0) are points on l1 and l2 respectively. so equations of the planes p1 containing l1 and p2 containing l2 are respectively x−2y z = 0 and x−2y z = −1. Explore math with our beautiful, free online graphing calculator. graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Find the distance from the point \(q=(1,1,3)\) to the line \(\vec\ell(t) = \langle 1, 1,1\rangle t\langle 2,3,1\rangle.\) solution the equation of the line gives us the point \(p=(1, 1,1)\) that lies on the line, hence \(\vec{pq} = \langle 0,2,2\rangle\). One has to solve the system of linear equations [\left[\begin{array}{ccc|c} 2&3& 2&7 \\ 1& 1& 3&5\end{array}\right]\nonumber\] as a vector equation [(\(x 1\vec{v} 1 x 2\vec{v} 2 \cdots x n\vec{v} n = \vec{b}\)): (but not collinear) vectors span a plane and not a 3 space, just as two collinear vectors span a line and not a plane. 1.

Solved 2 A 1 1 0 2 B 15 4 5 2 3 1 3 2 0 1 C Chegg H1,2,3i (the direction vectors of the two lines). so set ~n = h1,1,1i×h1,2,3i = h3− 2,−3 1,2−1i = h1,−2,1i. from above, we have found that (0,0,0) and (−1,0,0) are points on l1 and l2 respectively. so equations of the planes p1 containing l1 and p2 containing l2 are respectively x−2y z = 0 and x−2y z = −1. Explore math with our beautiful, free online graphing calculator. graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Find the distance from the point \(q=(1,1,3)\) to the line \(\vec\ell(t) = \langle 1, 1,1\rangle t\langle 2,3,1\rangle.\) solution the equation of the line gives us the point \(p=(1, 1,1)\) that lies on the line, hence \(\vec{pq} = \langle 0,2,2\rangle\). One has to solve the system of linear equations [\left[\begin{array}{ccc|c} 2&3& 2&7 \\ 1& 1& 3&5\end{array}\right]\nonumber\] as a vector equation [(\(x 1\vec{v} 1 x 2\vec{v} 2 \cdots x n\vec{v} n = \vec{b}\)): (but not collinear) vectors span a plane and not a 3 space, just as two collinear vectors span a line and not a plane. 1.

Solved 1 0 2 0 2 3 1 2 3 Let A D 1 Chegg Find the distance from the point \(q=(1,1,3)\) to the line \(\vec\ell(t) = \langle 1, 1,1\rangle t\langle 2,3,1\rangle.\) solution the equation of the line gives us the point \(p=(1, 1,1)\) that lies on the line, hence \(\vec{pq} = \langle 0,2,2\rangle\). One has to solve the system of linear equations [\left[\begin{array}{ccc|c} 2&3& 2&7 \\ 1& 1& 3&5\end{array}\right]\nonumber\] as a vector equation [(\(x 1\vec{v} 1 x 2\vec{v} 2 \cdots x n\vec{v} n = \vec{b}\)): (but not collinear) vectors span a plane and not a 3 space, just as two collinear vectors span a line and not a plane. 1.

Solved Question 1 A 2 5 B 2 5 C 3 D 3 Points Chegg
