
Solved Suppose X1 X2 X3 X4 And X5 Are Independent Normal Chegg Suppose that x1, x2, , xn are i.i.d random variables from a normal distribution with mean y and variance o?, where both u and oare unknown parameters. in class, we showed that x and s2 noi 2 1(x; x)2 are unbiased estimators of u and o , respectively (in fact, these results are true for any distribution, and not necessarily normal. Suppose x1;x2;¢¢¢ ;xn are i.i.d. random variables following b(n;p) distribution, where both n and p are unknown parameters. estimate them using the method of.

Solved Suppose X1 X2 Xn Are Independent Exponential Chegg Suppose that x1,x2, ,xn are i.i.d random variables on the interval [0,1] with density function: f(x|alpha) = [gamme(2alpha) [gamma(alpha)]^2] * [x(1 x)]^(alpha 1) where alpha > 0 is a parameter to be estimated from the sample. it can be shown that e[x] = 1 2. Let x1, x2 be a random sample from n(0, σ2) distribution, where σ > 0 and n(μ, σ2) denotes a normal distribution with mean μ and variance σ2. suppose, for some constant c, (c(x12 x22), ∞) is a confidence interval for variance σ2 with confidence coefficient 0.95. then the value of c is equal to. Suppose that x1, . . . , xn geom(p), i.e. the samples have. geometric distribution with parameter p. a geometric distribution is the distribution of the number of coin flips needed to see one head. write down the likelihood as a function of the observed data x1, . . . , xn, and the unknown parameter p. compute the mle of p. Assume you don't know y and you want to estimate it from the sample. let x(n) be the maximum of x1, x2, , xn. (a) show that for x = [0, 1], < x (1 p (952) 2. =r" (b) hence show that a 100(1 – a)% confidence interval for y is x(n).

1 Suppose X1 X2 Xn U What Is Fx1 X2 X Chegg Suppose that x1, . . . , xn geom(p), i.e. the samples have. geometric distribution with parameter p. a geometric distribution is the distribution of the number of coin flips needed to see one head. write down the likelihood as a function of the observed data x1, . . . , xn, and the unknown parameter p. compute the mle of p. Assume you don't know y and you want to estimate it from the sample. let x(n) be the maximum of x1, x2, , xn. (a) show that for x = [0, 1], < x (1 p (952) 2. =r" (b) hence show that a 100(1 – a)% confidence interval for y is x(n). Suppose that $x 1, x 2, \ldots, x n$ are i.i.d. random variables such that $x 1\sim n(\mu, 0.5)$ and $n = 100$. a) find a maximum number $c$ such that $$p(x 1\le c \mu, x 2\le c \mu, \ldots,x n\le. Problem 5: suppose x1 , , xn is a random sample generated from the normal distribution with mean μ and variance σ 2=1. 1. what is the probability density of x1 x2? 2. find the maximum likelihood estimate of μ. More specifically, suppose that xk = x0exp(r1 ∙ ∙ ∙ rk), where x0 is a fixed constant and r1, r2, . . . are i.i.d. n(μ, σ2). (a) find p(x2 > 1.3x0). (b) use (a.4) to find the density of x1. (c) find a formula for the 0.9 quantile of xk for all k. (d) what is the expected value of x2k for any k?. Let $x 1$, $x 2$, $x 3$, $\cdots$ be a sequence of i.i.d. $uniform(0,1)$ random variables. define the sequence $y n$ as \begin{align}%\label{} y n= \min (x 1,x 2, \cdots, x n). \end{align} prove the following convergence results independently (i.e, do not conclude the weaker convergence modes from the stronger ones). $y n \ \xrightarrow{d}\ 0$.
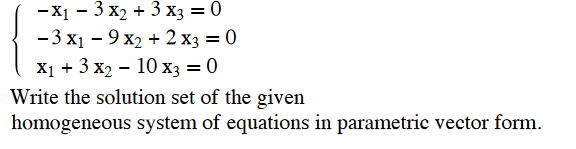
Solved X1 3 X2 3 X3 0 3 х1 9 х2 2 Xз D0 X1 3 X Chegg Suppose that $x 1, x 2, \ldots, x n$ are i.i.d. random variables such that $x 1\sim n(\mu, 0.5)$ and $n = 100$. a) find a maximum number $c$ such that $$p(x 1\le c \mu, x 2\le c \mu, \ldots,x n\le. Problem 5: suppose x1 , , xn is a random sample generated from the normal distribution with mean μ and variance σ 2=1. 1. what is the probability density of x1 x2? 2. find the maximum likelihood estimate of μ. More specifically, suppose that xk = x0exp(r1 ∙ ∙ ∙ rk), where x0 is a fixed constant and r1, r2, . . . are i.i.d. n(μ, σ2). (a) find p(x2 > 1.3x0). (b) use (a.4) to find the density of x1. (c) find a formula for the 0.9 quantile of xk for all k. (d) what is the expected value of x2k for any k?. Let $x 1$, $x 2$, $x 3$, $\cdots$ be a sequence of i.i.d. $uniform(0,1)$ random variables. define the sequence $y n$ as \begin{align}%\label{} y n= \min (x 1,x 2, \cdots, x n). \end{align} prove the following convergence results independently (i.e, do not conclude the weaker convergence modes from the stronger ones). $y n \ \xrightarrow{d}\ 0$.
