
Solved 5 14 Use Part 1 Of The Fundamental Theorem Of Chegg Use part 1 of the fundamental theorem of calculus to find the derivative of the function. g(y) = y your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. The fundamental theorem of calculus is d d x ∫ h (x) g (x) f (t) d t = f (g (x)) g ′ (x) − f (h (x)) h ′ (x). 1) g (x) = ∫ 1 x ln (3 t 2) d t.

Solved Use Part 1 Of The Fundamental Theorem Of Calculus To Chegg Solution: we apply the fundamental theorem of calculus. solution: the upper limit of integration is not x but x3. this result is not all that surprising. if we apply properties of the de nite integral, we see that y is constant and the derivative of a constant function is zero. and so we will use the chain rule to di¤erentiate it. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. the fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. the total area under a curve can be found using this formula. This video gives five examples of how to take the derivative of an integral using the fundamental theorem of calculus (ftc) part i. some examples involve using integral properties to. Part 1 establishes the relationship between differentiation and integration. if f(x) is continuous over an interval [a, b], and the function f(x) is defined by. then f ′ (x) = f(x) over (a, b). before we delve into the proof, a couple of subtleties are worth mentioning here.
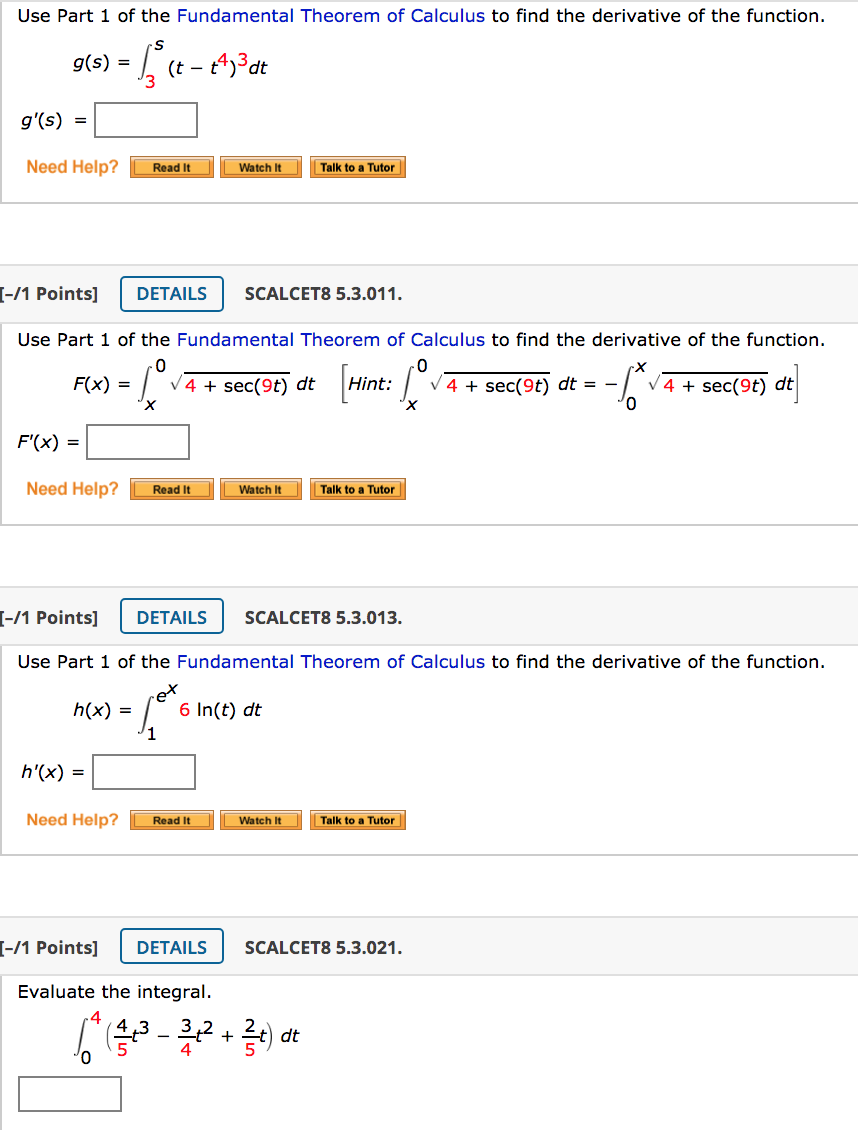
Solved Use Part 1 Of The Fundamental Theorem Of Calculus To Chegg This video gives five examples of how to take the derivative of an integral using the fundamental theorem of calculus (ftc) part i. some examples involve using integral properties to. Part 1 establishes the relationship between differentiation and integration. if f(x) is continuous over an interval [a, b], and the function f(x) is defined by. then f ′ (x) = f(x) over (a, b). before we delve into the proof, a couple of subtleties are worth mentioning here. The fundamental theorem of calculus is appropriately named because it establishes a connection between the two branches of calculus: differential calculus and integral calculus. differential calculus arose from the tangent problem, whereas integral calcu. lus arose from a seemingly unrelated problem, the area problem. State the meaning of the fundamental theorem of calculus, part 1. use the fundamental theorem of calculus, part 1, to evaluate derivatives of integrals. state the meaning of the fundamental theorem of calculus, part 2. use the fundamental theorem of calculus, part 2, to evaluate definite integrals. Use the fundamental theorem of calculus, part 1, to evaluate derivatives of integrals. state the meaning of the fundamental theorem of calculus, part 2. use the fundamental theorem of calculus, part 2, to evaluate definite integrals. explain the relationship between differentiation and integration. This worksheet focuses on the rst part. the fundamental theorem of calculus (ftc), part 1 suppose that f(x) is a continuous function over a closed interval a x b. then z b a f(x)dx = f(b) f(a); where fis any antiderivative of f. some important notes concerning part 1 of the ftc: (i) the rst part of the ftc will be used over and over again.

Solved 1 Point The Fundamental Theorem Of Calculus Use Chegg The fundamental theorem of calculus is appropriately named because it establishes a connection between the two branches of calculus: differential calculus and integral calculus. differential calculus arose from the tangent problem, whereas integral calcu. lus arose from a seemingly unrelated problem, the area problem. State the meaning of the fundamental theorem of calculus, part 1. use the fundamental theorem of calculus, part 1, to evaluate derivatives of integrals. state the meaning of the fundamental theorem of calculus, part 2. use the fundamental theorem of calculus, part 2, to evaluate definite integrals. Use the fundamental theorem of calculus, part 1, to evaluate derivatives of integrals. state the meaning of the fundamental theorem of calculus, part 2. use the fundamental theorem of calculus, part 2, to evaluate definite integrals. explain the relationship between differentiation and integration. This worksheet focuses on the rst part. the fundamental theorem of calculus (ftc), part 1 suppose that f(x) is a continuous function over a closed interval a x b. then z b a f(x)dx = f(b) f(a); where fis any antiderivative of f. some important notes concerning part 1 of the ftc: (i) the rst part of the ftc will be used over and over again.
