Solved 52 Iii A Hammer Thrower Accelerates The Hammer Of Chegg

Solved 52 Iii A Hammer Thrower Accelerates The Hammer Of Chegg The equation solver allows you to enter your problem and solve the equation to see the result. solve in one variable or many. Instantly solve any math word problem with clear, step by step solutions.
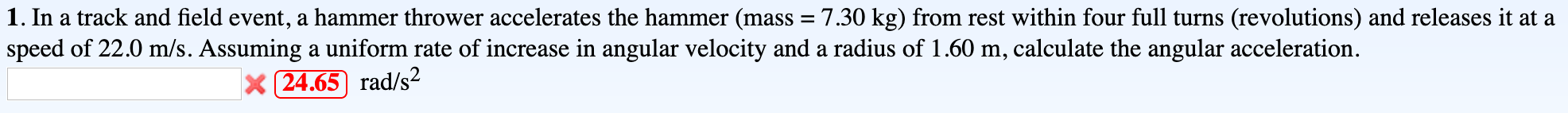
Solved 1 In A Track And Field Event A Hammer Thrower Chegg Free math problem solver answers your algebra homework questions with step by step explanations. Isolved people cloud is an intuitive platform that simplifies hr processes, payroll, and workforce management for businesses of all sizes. To solve your equation using the equation solver, type in your equation like x 4=5. the solver will then show you the steps to help you learn how to solve it on your own. Free equations calculator solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps. type in any equation to get the solution, steps and graph.
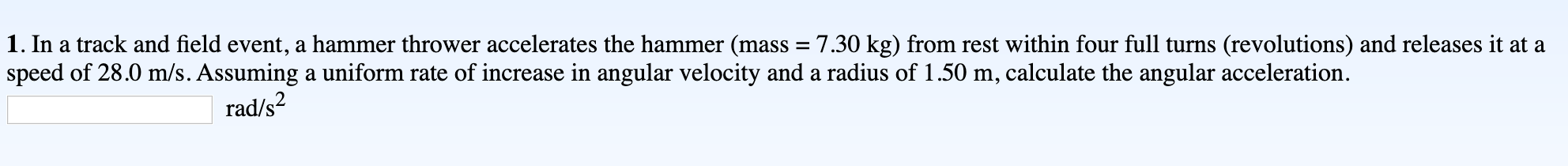
Solved 1 In A Track And Field Event A Hammer Thrower Chegg To solve your equation using the equation solver, type in your equation like x 4=5. the solver will then show you the steps to help you learn how to solve it on your own. Free equations calculator solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps. type in any equation to get the solution, steps and graph. This online math solver can tell you the answer for your math problem or word problem, and even show you the steps. The meaning of solve is to find a solution, explanation, or answer for. how to use solve in a sentence. Solved definition: 1. past simple and past participle of solve 2. to find an answer to a problem: . learn more. Mystery solved: the truth behind tuesday night’s strange sky lights b95.5 maglev’s ‘tunnel boom’ might be solved – but other issues mean it’s unlikely to come to uk institution of mechanical engineers maglev’s ‘tunnel boom’ might be solved – but other issues mean it’s unlikely to come to uk institution of mechanical.
Comments are closed.