
Solved 55 It Is Given That U1 1 U2 U3 6 And Chegg To find the approximate value of u4 using lagrange's inter 55. it is given that u1 =1,u2 u3 = 6 and u4 u5 u6 u7 u8 =30. what is the approximate value of u4 when computed by using lagrange's interpolation formula ? (a) 7 (b) 6 (c) 5 (d) 4 56. let f (x)=5x3−13x2 11x 4. Problem: given $u 1 = 1, u 2 u 3 = 6$ and $u 4 u 5 u 6 u 7 u 8 = 30.$ what is the approximate value of $u 4$ when computed by using lagrange's interpolation formula? i tried to solve it as.

Solved Let U1 вћјвћўв 61в 6261вћ вћ And U2 вћјвћўв 305302в 301вћ вћ Note That Chegg The sequence u1 u2 u3 is defined by the recurrence relation un 1 = (un)^2 1, n> or equal to 1 given that u1=k, where k is constant (a) find expressions for u2 and u3 in terms of k i got u3=k^2 1 and u4=k^4 1 if anyone can confirm these that would be great problem is part two b) find the possible values of k when u2 u3 = 11 i ended up with k. Provided that u1=(2,4,3),u2=(2,4,2) and u3=(−6,4,2), write v=(54,12,9) as a linear combination of u1,u2, and u3, if possible. v=3u1 6u2−6u3v=4u1 7u2−7u3 it is not possible to write v as a linear combination of u1,u2, and u3. v=4u1−7u2−7u3v=3u1−6u2−6u3. Let u1 = (1, 2, 3), u2 = (2, 1, 3), u3 = (6, 1, x), and v = (1, 1, 1). calculate the coordinates of v with respect to the basis b = {u1, u2, u3} (if it is possible). (b) let e1, e2, e3, and e4 be some vectors in a vector space v, and suppose that (e1, e2, e3, e4) are linearly independent. It is given that v = [0 5 3 0], u 1 = [1 1 2 2], u 2 = [2 3 5 6], u 3 = [− 3 1 − 4 2] explanation: to express v as a linear combination of u 1 , u 2 and u 3 , we need to find coefficients a , b and c s.

Solved Solve For U 16 U 35 Chegg Let u1 = (1, 2, 3), u2 = (2, 1, 3), u3 = (6, 1, x), and v = (1, 1, 1). calculate the coordinates of v with respect to the basis b = {u1, u2, u3} (if it is possible). (b) let e1, e2, e3, and e4 be some vectors in a vector space v, and suppose that (e1, e2, e3, e4) are linearly independent. It is given that v = [0 5 3 0], u 1 = [1 1 2 2], u 2 = [2 3 5 6], u 3 = [− 3 1 − 4 2] explanation: to express v as a linear combination of u 1 , u 2 and u 3 , we need to find coefficients a , b and c s. Linear combination of u1 , u2, and u3 . here’s the best way to solve it. start by setting up the equation v = (41, 5, 12) as a linear combination of u 1, u 2, and u 3 using scalars a, b, and c: v = a ⋅ u 1 b ⋅ u 2 c ⋅ u 3. not the question you’re looking for? post any question and get expert help quickly. Let r3 have the euclidean inner product. use the gram–schmidt process to transform. the basis {u1, u2, u3} into an orthonormal basis. it is given that u 1 = 1 , 0 , 0 u 2 = 3 , 7 , 2 u 3 = 0 , 4 , 1 step 1: consider v 1 = u 1 = 1 , 0 , determine the dimension of and a basis for the solution space of the system. We have an arithmetic sequence \(u 1, u 2, u 3, \ldots\) with the first term \(u 1 = 1\) and a common difference \(d\) which is not equal to 0. it is also given that \(u 2, u 3,\) and \(u 6\) form a geometric sequence. show more…. To solve it show that an arbitrary vectorsl v= (a,b,c) \in ∈ r 3 is a linear combination of u 1,u 2 u1,u2 and u 3 u3 . let. v=xu 1 yu 2 zu 3 v = xu1 yu2 zu3. hence, (a,b,c)=x (1,1,1) y (1,2,3) z (1,5,8) (a,b,c) = x(1,1,1) y(1,2,3) z(1,5,8) resolve as. x y z=a x y z = a. x 2y 5z=b x 2y 5z = b. x 3y 8z=c x 3y 8z = c.
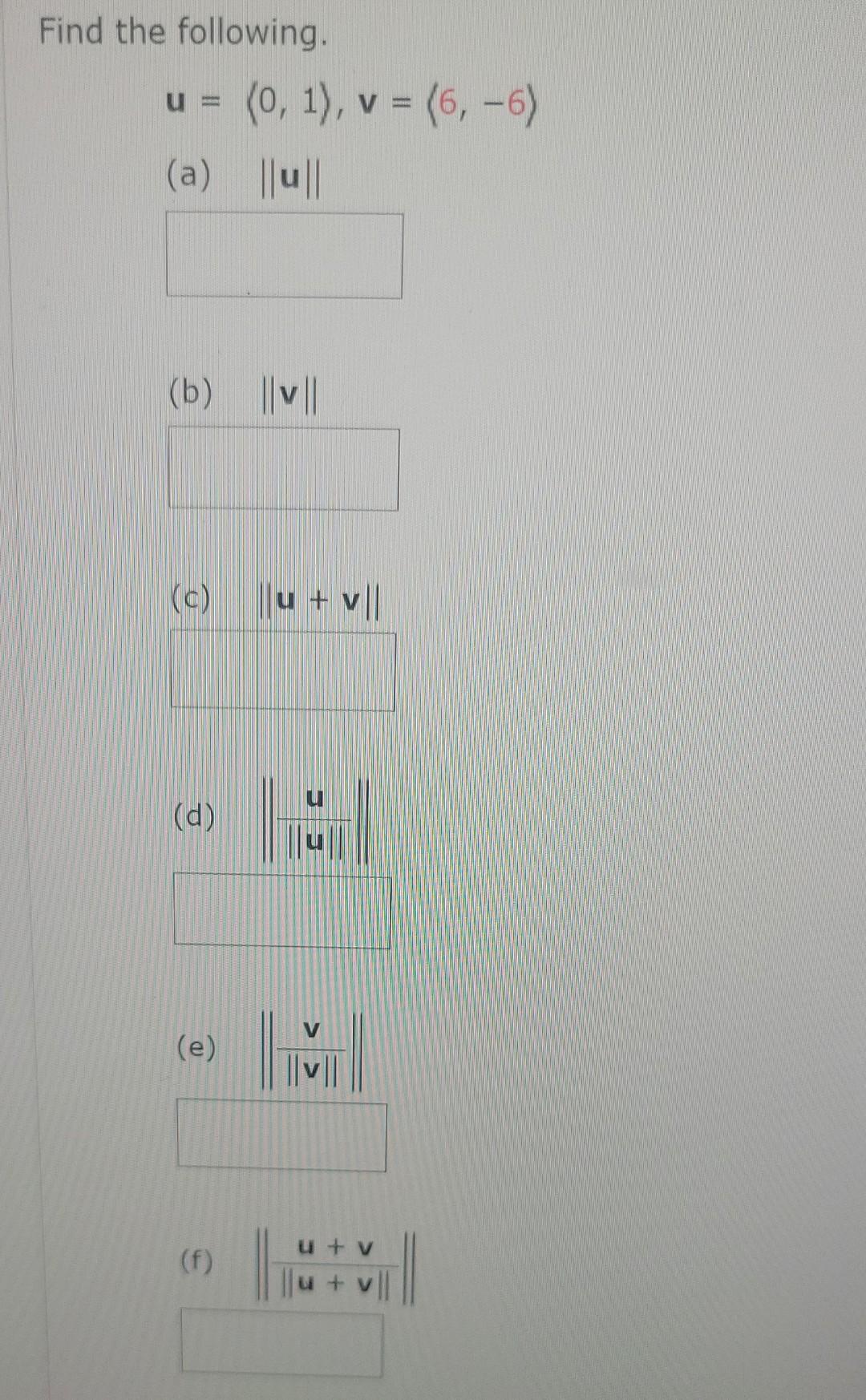
Solved Find The Following U 0 1 V 6 в 6 A в ґuв ґ B в ґvв ґ Chegg Linear combination of u1 , u2, and u3 . here’s the best way to solve it. start by setting up the equation v = (41, 5, 12) as a linear combination of u 1, u 2, and u 3 using scalars a, b, and c: v = a ⋅ u 1 b ⋅ u 2 c ⋅ u 3. not the question you’re looking for? post any question and get expert help quickly. Let r3 have the euclidean inner product. use the gram–schmidt process to transform. the basis {u1, u2, u3} into an orthonormal basis. it is given that u 1 = 1 , 0 , 0 u 2 = 3 , 7 , 2 u 3 = 0 , 4 , 1 step 1: consider v 1 = u 1 = 1 , 0 , determine the dimension of and a basis for the solution space of the system. We have an arithmetic sequence \(u 1, u 2, u 3, \ldots\) with the first term \(u 1 = 1\) and a common difference \(d\) which is not equal to 0. it is also given that \(u 2, u 3,\) and \(u 6\) form a geometric sequence. show more…. To solve it show that an arbitrary vectorsl v= (a,b,c) \in ∈ r 3 is a linear combination of u 1,u 2 u1,u2 and u 3 u3 . let. v=xu 1 yu 2 zu 3 v = xu1 yu2 zu3. hence, (a,b,c)=x (1,1,1) y (1,2,3) z (1,5,8) (a,b,c) = x(1,1,1) y(1,2,3) z(1,5,8) resolve as. x y z=a x y z = a. x 2y 5z=b x 2y 5z = b. x 3y 8z=c x 3y 8z = c.

Solved Which They Are Given U1 32 31 U2 2646 26412 Chegg We have an arithmetic sequence \(u 1, u 2, u 3, \ldots\) with the first term \(u 1 = 1\) and a common difference \(d\) which is not equal to 0. it is also given that \(u 2, u 3,\) and \(u 6\) form a geometric sequence. show more…. To solve it show that an arbitrary vectorsl v= (a,b,c) \in ∈ r 3 is a linear combination of u 1,u 2 u1,u2 and u 3 u3 . let. v=xu 1 yu 2 zu 3 v = xu1 yu2 zu3. hence, (a,b,c)=x (1,1,1) y (1,2,3) z (1,5,8) (a,b,c) = x(1,1,1) y(1,2,3) z(1,5,8) resolve as. x y z=a x y z = a. x 2y 5z=b x 2y 5z = b. x 3y 8z=c x 3y 8z = c.

Solved Given U1 U2 Chegg
