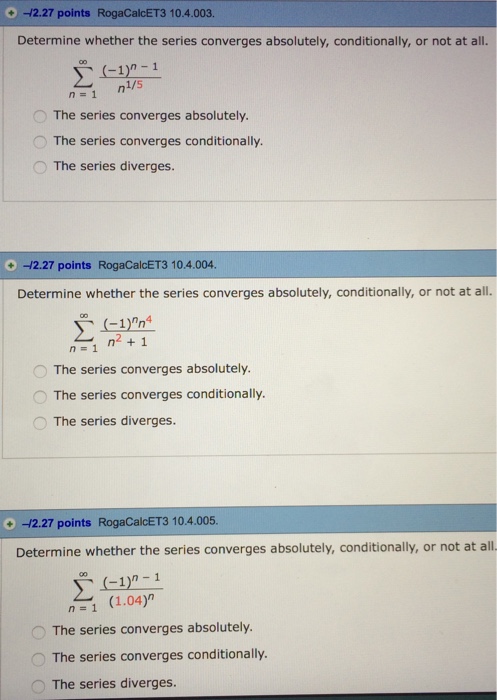
Solved Determine Whether The Series Converges Absolutely Chegg Determine whether the series is absolutely convergent, conditional convergent or divergent. make sure to show detail step by step solutions. mnke sure to name the test that you are using to do this probtem, example: integral test, comparison test, altemating series test, root test, etc. ∑ n = 2 ∞ n 3 1 ( − 1 ) n 1. Absolute convergence occurs when the sum of the absolute values of a series' terms converges. in other words, if the series \(\sum {n=1}^{\infty} a n\) is such that \(\sum {n=1}^{\infty} |a n|\) is convergent, then we say the original series is absolutely convergent.

Solved Determine Whether The Series Is Absolutely Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. there are 3 steps to solve this one. 8) determine whether the series is absolutely convergent, conditionally convergent, or divergent. ∑n=2∞ (−1)n n lnn1 9) determine whether the series satisfies conditions of the alternating series (ast). 16. determine whether the series x∞ n=1 n2 n3 1 is convergent or divergent. answer: if we let f(x) = x2 x3 1, then the terms of the series and the function f satisfy the hypotheses of the integral test, so the series will converge if and only if z ∞ 1 f(x)dx = z ∞ 1 x2 x3 1 dx is finite. In this section we will discuss using the ratio test to determine if an infinite series converges absolutely or diverges. the ratio test can be used on any series, but unfortunately will not always yield a conclusive answer as to whether a series will converge absolutely or diverge. We need to determine if the series \( \sum {n=1}^{\infty}( 1)^{n} n \sin \frac{1}{n} \) is absolutely convergent, conditionally convergent, or divergent. to do this, we can consider the behavior of the terms as the series progresses.

Solved Problem Set No 8 1 Determine Whether The Series Is Chegg In this section we will discuss using the ratio test to determine if an infinite series converges absolutely or diverges. the ratio test can be used on any series, but unfortunately will not always yield a conclusive answer as to whether a series will converge absolutely or diverge. We need to determine if the series \( \sum {n=1}^{\infty}( 1)^{n} n \sin \frac{1}{n} \) is absolutely convergent, conditionally convergent, or divergent. to do this, we can consider the behavior of the terms as the series progresses. Determine whether the series is absolutely convergent, conditional convergent or divergent. make sure to show detail step by step solutions. make sure to name the test that you are using to do this problem, example: integral test, comparison test, alternating series test, root test, etc. ∑ n = 2 ∞ n 3 1 ( − 1 ) n 1. If we have \(\sum {n=1}^{\infty} a n\), then the series converges absolutely if \(\sum {n=1}^{\infty} |a n|\) is convergent. in our specific problem, we checked for absolute convergence by considering \(\sum {n=1}^{\infty} |( 3 4)^n n|\), which simplifies to \(\sum {n=1}^{\infty} (3 4)^n n\). For each given series, state whether it is absolutely convergent, conditionally convergent, or divergent. justify your answer. solved by expert hoan nguyen 05 29 2024. step 1. this is a harmonic series which is known to be divergent. we can prove this using the integral test. the integral from 1 to ∞ of (2x 1) x dx is divergent, therefore. Free series convergence calculator test infinite series for convergence step by step.

Solved In Exercises 1 8 Determine Whether The Series Is Chegg Determine whether the series is absolutely convergent, conditional convergent or divergent. make sure to show detail step by step solutions. make sure to name the test that you are using to do this problem, example: integral test, comparison test, alternating series test, root test, etc. ∑ n = 2 ∞ n 3 1 ( − 1 ) n 1. If we have \(\sum {n=1}^{\infty} a n\), then the series converges absolutely if \(\sum {n=1}^{\infty} |a n|\) is convergent. in our specific problem, we checked for absolute convergence by considering \(\sum {n=1}^{\infty} |( 3 4)^n n|\), which simplifies to \(\sum {n=1}^{\infty} (3 4)^n n\). For each given series, state whether it is absolutely convergent, conditionally convergent, or divergent. justify your answer. solved by expert hoan nguyen 05 29 2024. step 1. this is a harmonic series which is known to be divergent. we can prove this using the integral test. the integral from 1 to ∞ of (2x 1) x dx is divergent, therefore. Free series convergence calculator test infinite series for convergence step by step.

Solved Determine Whether The Series Is Absolutely Chegg For each given series, state whether it is absolutely convergent, conditionally convergent, or divergent. justify your answer. solved by expert hoan nguyen 05 29 2024. step 1. this is a harmonic series which is known to be divergent. we can prove this using the integral test. the integral from 1 to ∞ of (2x 1) x dx is divergent, therefore. Free series convergence calculator test infinite series for convergence step by step.
