
Solved Prove Chegg Answer to 9. (a) prove that for any x1 and. Proof by contraposition example: prove that for any integers x and y, if xy is even then either x is even ory is even. proof by contraposition: suppose x and y are both odd integers. then by definition of odd, there exist integers a and b such that x = 2a 1 and y = 2b 1.

Solved Prove Chegg Suppose that we have independent and identically distributed (i.i.d.) random variables x1, x2, x3 . with finite mean e[x1] =and variance var(xi) = 02. let s = x1 x,. prove that for any fixed & > 0 and 1 2. (cauchy schwarz inequality) prove that for any x,yinrn|xty|≤||x||2||y||2and equality holds if and only if x and y are linearly dependent. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Prove the following statement using mathe matical induction. (1 x)" > 1 nx problem 2 prove the following using the specified technique: (a) prove by contrapositive that for any two real numbers, x and y, if x is rational and y is irrational then x y is also irrational. y, (b) prove by. Question: d. prove that if r1 is a transitive relation on a, then r1@r1 must also be transitive.e. suppose that r1 is transitive relation's on a and a∩b=0. prove, that r,=r1∪a×b∪b×b is a transitive relation on a∪b. (hint if (x,y),(y,z)inr. what are the possibilities for what set each of x1,y,z came from?).

Solved Prove Chegg Prove the following statement using mathe matical induction. (1 x)" > 1 nx problem 2 prove the following using the specified technique: (a) prove by contrapositive that for any two real numbers, x and y, if x is rational and y is irrational then x y is also irrational. y, (b) prove by. Question: d. prove that if r1 is a transitive relation on a, then r1@r1 must also be transitive.e. suppose that r1 is transitive relation's on a and a∩b=0. prove, that r,=r1∪a×b∪b×b is a transitive relation on a∪b. (hint if (x,y),(y,z)inr. what are the possibilities for what set each of x1,y,z came from?). Prove that, for any x1, , xn, nn v(a x1 anxn ΣΣαρα(x a;a;cov(x;,x;) i=1 j=1 your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. (3 points) prove that for any x0,x1,⋯xn and for any x, we have ∑i=0nℓi(x)=1, where ℓi(x)=∏j=0,j =in(xi−xjx−xj). (hint, show that ∑i=0nℓi(x) is the interpolating polynomial for the following table.) \begin{tabular}{c|cccc} x & x0 & x1 & ⋯ & xn \\ \hliney & 1 & 1 & ⋯ & 1 \end{tabular}. Use the principle of mathematical induction to verify that, for n any positive integer, 6n 1 is divisible by 5. solution. for any n 1, let pn be the statement that 6n 1 is divisible by 5. base case. the statement p1 says that 61 1 = 6 1 = 5 is divisible by 5, which is true. inductive step. fix k 1, and suppose that pk holds, that is, 6k 1 is. Let x> −1 x> − 1 and n n be a positive integer. prove bernoulli's inequality: (1 x)n ≥ 1 nx (1 x) n ≥ 1 n x. proof: base case: for n = 1 n = 1, 1 x = 1 x 1 x = 1 x so the inequality holds. induction assumption: assume that for some integer k ≥ 1 k ≥ 1, (1 x)k ≥ 1 kx (1 x) k ≥ 1 k x.

Solved Prove Chegg Prove that, for any x1, , xn, nn v(a x1 anxn ΣΣαρα(x a;a;cov(x;,x;) i=1 j=1 your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. (3 points) prove that for any x0,x1,⋯xn and for any x, we have ∑i=0nℓi(x)=1, where ℓi(x)=∏j=0,j =in(xi−xjx−xj). (hint, show that ∑i=0nℓi(x) is the interpolating polynomial for the following table.) \begin{tabular}{c|cccc} x & x0 & x1 & ⋯ & xn \\ \hliney & 1 & 1 & ⋯ & 1 \end{tabular}. Use the principle of mathematical induction to verify that, for n any positive integer, 6n 1 is divisible by 5. solution. for any n 1, let pn be the statement that 6n 1 is divisible by 5. base case. the statement p1 says that 61 1 = 6 1 = 5 is divisible by 5, which is true. inductive step. fix k 1, and suppose that pk holds, that is, 6k 1 is. Let x> −1 x> − 1 and n n be a positive integer. prove bernoulli's inequality: (1 x)n ≥ 1 nx (1 x) n ≥ 1 n x. proof: base case: for n = 1 n = 1, 1 x = 1 x 1 x = 1 x so the inequality holds. induction assumption: assume that for some integer k ≥ 1 k ≥ 1, (1 x)k ≥ 1 kx (1 x) k ≥ 1 k x.
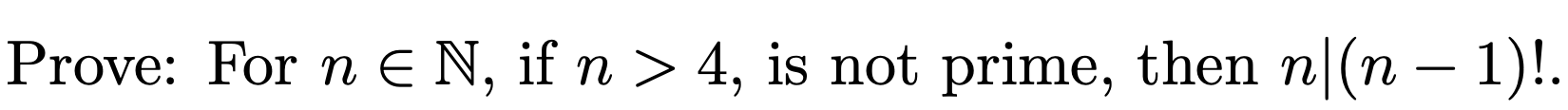
Solved Prove Chegg Use the principle of mathematical induction to verify that, for n any positive integer, 6n 1 is divisible by 5. solution. for any n 1, let pn be the statement that 6n 1 is divisible by 5. base case. the statement p1 says that 61 1 = 6 1 = 5 is divisible by 5, which is true. inductive step. fix k 1, and suppose that pk holds, that is, 6k 1 is. Let x> −1 x> − 1 and n n be a positive integer. prove bernoulli's inequality: (1 x)n ≥ 1 nx (1 x) n ≥ 1 n x. proof: base case: for n = 1 n = 1, 1 x = 1 x 1 x = 1 x so the inequality holds. induction assumption: assume that for some integer k ≥ 1 k ≥ 1, (1 x)k ≥ 1 kx (1 x) k ≥ 1 k x.
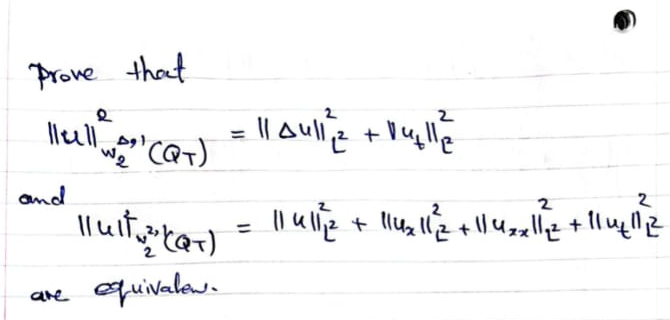
Solved Prove That Chegg
