
Solved 9 In How Many Ways Can 3 Identical Math Books 4 Chegg [3] 12. from a class of 15 women and 10 men, a group of 6 students is chosen to act as class representatives. how many different selections of these 6 students are possible if: [6] a. there are no restrictions? b. no men are chosen? c. 4 women and 2 men are chosen?. You use permutations to solve this because we are talking about different arrangements here. since there are 4 mathematics books you can arrange those 4 using = 4! 3 chemistry books you can arrange that bundle using = 3!.
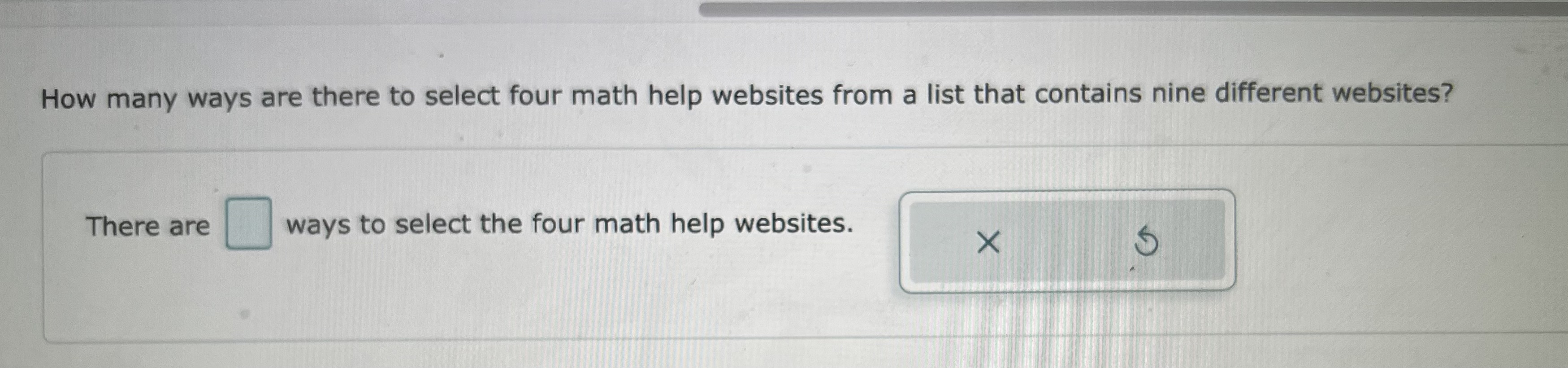
Solved How Many Ways Are There To Select Four Math Help Chegg Thus there are 4 units which can be arranged in 4! = 24 ways. now in each of arrangements. mathematics books can be arranged in 3! ways, history books in 4! ways, chemistry books in 3! ways. and biology books in 2! ways. thus the total number of ways = 4! × 3! × 4! × 3! × 2! = 41472. Suppose we have 3 distinct people, 4 identical math books, and 5 identical history books. a) b) how many different (distinguishable) ways can all the books be distributed to the students? 3!⋅4!5! 5!3!⋅4!. We have 4 identical math books and 3 identical science books. the total number of books is 7. if all books were distinct, there would be 7! ways to arrange them. however, since the math books are identical and the science books are identical, we must divide by the number of ways to arrange the identical books. Calculate the total number of books: 3 (math) 4 (chemistry) = 7 books. use the formula for arrangements of identical objects: total arrangements = 7! (3! * 4!) calculate 7! = 5040, 3! = 6, and 4! = 24.

Be Sure To Explain Your Solutions 4 How Many Ways Chegg We have 4 identical math books and 3 identical science books. the total number of books is 7. if all books were distinct, there would be 7! ways to arrange them. however, since the math books are identical and the science books are identical, we must divide by the number of ways to arrange the identical books. Calculate the total number of books: 3 (math) 4 (chemistry) = 7 books. use the formula for arrangements of identical objects: total arrangements = 7! (3! * 4!) calculate 7! = 5040, 3! = 6, and 4! = 24. 1 identify the total number of items to be arranged, which is the sum of the math books and science books, which is 4 3 = 7 books. Number of maths book = 4. number of physics books = 3. number of chemistry books = 2. number of biology books = 1. since we want books of the same subjects together . we have to treat all maths books as 1 unit . all physics books as 1 unit. all chemistry books as 1 unit . and all biology books as 1 unit. now the total number of units = 4. In how many ways can 3 identical math books, 4 identical chemistry books, and 3 identical biology books be arranged on a shelf? [2] your solution’s ready to go! enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. Hint: first compute how many possibilities you have of choosing 3 math books out of 7, 2 history books out of 4 and 3 fiction books out of 5. now multiply by the number of ways you can place 8 books on a shelf.

In How Many Ways Can 4 Books Of Mathematics And 3 Books Of English Can 1 identify the total number of items to be arranged, which is the sum of the math books and science books, which is 4 3 = 7 books. Number of maths book = 4. number of physics books = 3. number of chemistry books = 2. number of biology books = 1. since we want books of the same subjects together . we have to treat all maths books as 1 unit . all physics books as 1 unit. all chemistry books as 1 unit . and all biology books as 1 unit. now the total number of units = 4. In how many ways can 3 identical math books, 4 identical chemistry books, and 3 identical biology books be arranged on a shelf? [2] your solution’s ready to go! enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. Hint: first compute how many possibilities you have of choosing 3 math books out of 7, 2 history books out of 4 and 3 fiction books out of 5. now multiply by the number of ways you can place 8 books on a shelf.
