Solved A And B Are In Direct Proportion The Equation Of α and b are in direct proportion. the equation of proportionality is n=60. work out the value of a when b=4. if your answer is a decimal, give it to 1 d.p. revious. Since $$a$$ a and $$b$$ b are in direct proportion, we can express this relationship as $$\frac{a}{b} = k$$ b a = k, where $$k$$ k is a constant. from the equation of proportionality, we have $$a = 8$$ a = 8. substitute $$a$$ a into the proportionality equation: $$\frac{8}{b} = k$$ b 8 = k. to find $$k$$ k, we need to determine $$b$$ b when $$a.
Solved A And B Are In Direct Proportion The Equation Of When b is 4, and a is in direct proportion to b with the proportionality equation a=8b, the value of a is calculated to be 32 by multiplying 8 by 4. explanation: you are asked to calculate the value of a when b equals 4, and you know that a and b are in direct proportion with the equation of proportionality being a=8b. In order to work out an unknown value given a directly proportional relationship: write down the direct proportion formula. determine the value of \textbf {k} . substitute \textbf {k} and the known value into the direct proportion formula. solve the equation. get your free direct proportion worksheet of 20 questions and answers. The solution follows the direct proportionality principle where the value of a is directly derived from b using a constant factor of 8, confirming the relationship established by the equation. heart outlined. Direct and inverse proportions are two important basic concepts of algebra in mathematics. these concepts are useful in identifying the relationship between two quantities and establishing the equation for the same. solving direct and inverse proportion questions will help you to solve many real world.
Solved A And B Are In Direct Proportion The Equation Of The solution follows the direct proportionality principle where the value of a is directly derived from b using a constant factor of 8, confirming the relationship established by the equation. heart outlined. Direct and inverse proportions are two important basic concepts of algebra in mathematics. these concepts are useful in identifying the relationship between two quantities and establishing the equation for the same. solving direct and inverse proportion questions will help you to solve many real world. Direct proportion is denoted by the proportionality symbol (∝). for example, if the variables a and b are proportional to each other, we can represent this as a∝b. if we replace the proportionality sign with the equal sign, the equation changes to: $latex a= kb$ where k is called a constant of proportionality. In a direct proportion, two variables are related in such a way that the ratio of their values remains constant. the equation of proportionality is given as a =8b. to find the value of a when b=4, we substitute b with 4 in the equation. identify the equation of proportionality: a= 8b. substitute b=4 into the equation: a =8⋅4. ‘if “a” and “b” are in direct proportion, then (a – 1) and (b – 1) are also in direct proportion”. solution: the given statement is “false” justification: we know that, if “a” and “b” are in direct proportion, we can write . a b = k . let us assume that a = 2 and b = 4 . hence, a b = 2 4 = 1 2 …(1). Other forms of direct proportion. not all quantities x and y are in direct proportion. study the following example. it is given that variables x and y are related by the equation y = 5x 2. complete the table below.

Proportion Inverse Proportion Derive Equation Grade Onmaths My Xxx Direct proportion is denoted by the proportionality symbol (∝). for example, if the variables a and b are proportional to each other, we can represent this as a∝b. if we replace the proportionality sign with the equal sign, the equation changes to: $latex a= kb$ where k is called a constant of proportionality. In a direct proportion, two variables are related in such a way that the ratio of their values remains constant. the equation of proportionality is given as a =8b. to find the value of a when b=4, we substitute b with 4 in the equation. identify the equation of proportionality: a= 8b. substitute b=4 into the equation: a =8⋅4. ‘if “a” and “b” are in direct proportion, then (a – 1) and (b – 1) are also in direct proportion”. solution: the given statement is “false” justification: we know that, if “a” and “b” are in direct proportion, we can write . a b = k . let us assume that a = 2 and b = 4 . hence, a b = 2 4 = 1 2 …(1). Other forms of direct proportion. not all quantities x and y are in direct proportion. study the following example. it is given that variables x and y are related by the equation y = 5x 2. complete the table below.
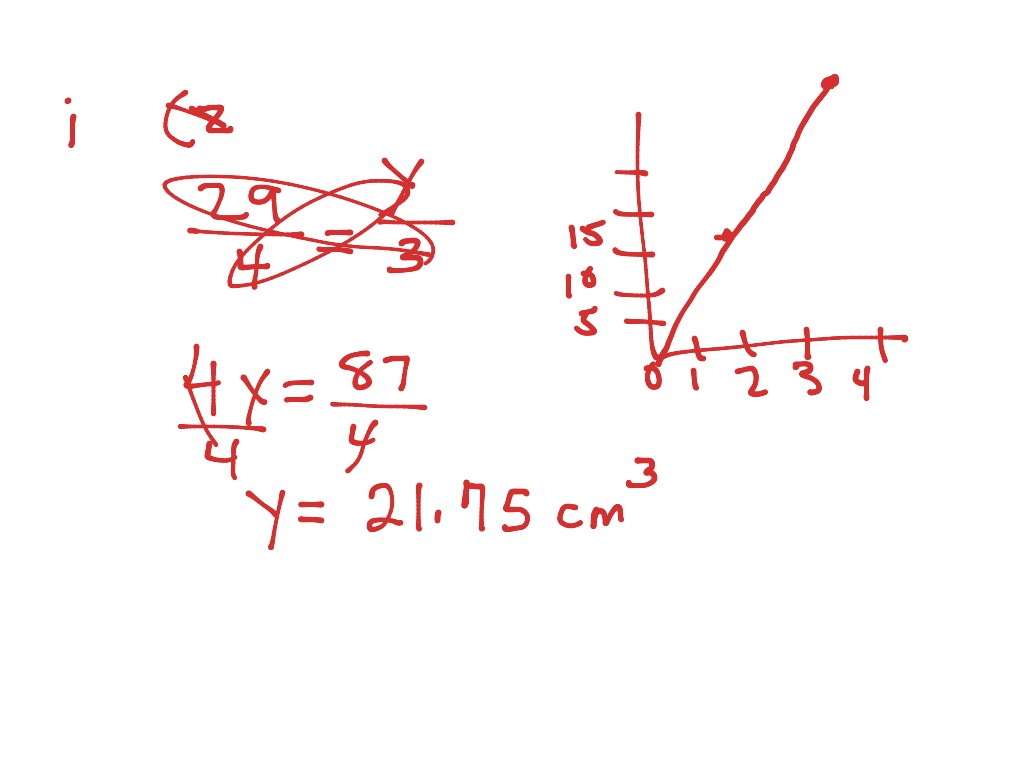
Showme Direct Proportion ‘if “a” and “b” are in direct proportion, then (a – 1) and (b – 1) are also in direct proportion”. solution: the given statement is “false” justification: we know that, if “a” and “b” are in direct proportion, we can write . a b = k . let us assume that a = 2 and b = 4 . hence, a b = 2 4 = 1 2 …(1). Other forms of direct proportion. not all quantities x and y are in direct proportion. study the following example. it is given that variables x and y are related by the equation y = 5x 2. complete the table below.
Showme Direct Proportion
