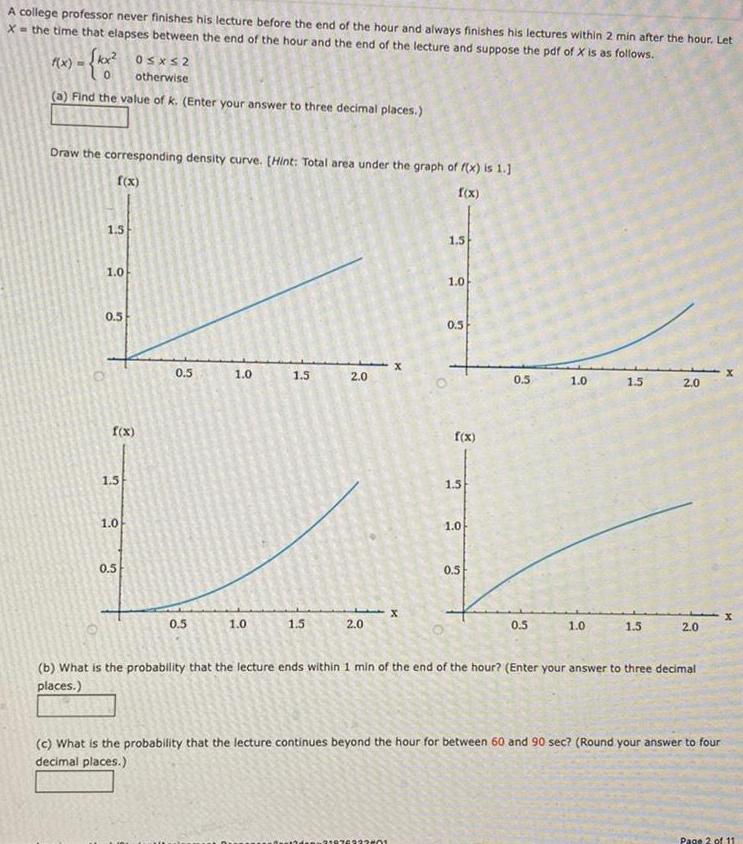
Answered A College Professor Never Finishes His Lecture Before The A college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let x = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of x is as follows. f(x) i kox? osxs2 otherwise (a) find the value of k. A college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 minutes after the hour. let x be the time that elapses between the end of the hour and the end of the lecture, and suppose the pdf of x is as follows:.
A College Professor Never Finishes His Lecture Before The End Of The The length of time a professor lectures during his class has a continuous uniform probability distribution between 46 minutes and 60 minutes. let x= the length of lecture in minutes. suppose one of the professor's lectures is randomly selected. find each probability. drawing a sketch may be helpful. The given problem is asking for the probability that the lecture continues beyond the hour for between 60 and 90 seconds. we can solve this problem by finding the probability that x, the time that elapses between the end of the hour and the end of the lecture, is between 60 and 90 seconds. A college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let x = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of x is as follows. A college professor never finishes his lecture before the end of the hour and always finishes his lectures within $2 \mathrm{~min}$ after the hour. let $x=$ the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of $x$ is $$ f(x)=\left\{\begin{array}{cc} k x^{2} & 0 \leq x \leq 2 \\ 0 & \text { otherwise }.
Solved A College Professor Never Finishes His Lecture Before The End A college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let x = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of x is as follows. A college professor never finishes his lecture before the end of the hour and always finishes his lectures within $2 \mathrm{~min}$ after the hour. let $x=$ the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of $x$ is $$ f(x)=\left\{\begin{array}{cc} k x^{2} & 0 \leq x \leq 2 \\ 0 & \text { otherwise }. Example 3 (exercise 5) a college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let the rv x denote the extra time he takes. suppose the pdf of x is. otherwise. find the value of k and draw the corresponding density curve. First, we need to find the value of c. since the professor always finishes his lectures within 2 minutes (120 seconds) after the hour, the range of x is [0, 120]. the pdf of x is a constant function, so the area under the curve must be equal to 1. College professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let x = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of x is as follows. A college lecturer never finishes his lecture before the end of the hour and always finishes his lecture within 2 min after the hour. let x= the time that elapses between the end of the hour and the end of the.
Solved A College Professor Never Finishes His Lecture Before The End Example 3 (exercise 5) a college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let the rv x denote the extra time he takes. suppose the pdf of x is. otherwise. find the value of k and draw the corresponding density curve. First, we need to find the value of c. since the professor always finishes his lectures within 2 minutes (120 seconds) after the hour, the range of x is [0, 120]. the pdf of x is a constant function, so the area under the curve must be equal to 1. College professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let x = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of x is as follows. A college lecturer never finishes his lecture before the end of the hour and always finishes his lecture within 2 min after the hour. let x= the time that elapses between the end of the hour and the end of the.

Answered A College Professor Never Finishes His Bartleby College professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let x = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of x is as follows. A college lecturer never finishes his lecture before the end of the hour and always finishes his lecture within 2 min after the hour. let x= the time that elapses between the end of the hour and the end of the.
