A College Professor Never Finishes His Lecture Before The End Of The Question: a college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let x = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of x is as follows. f(x) i kox? osxs2 otherwise (a) find the value of k. To solve the problem, we need to assume a probability density function (pdf) for $$x$$x. since $$x$$x is the time that elapses between the end of the hour and the end of the lecture, we can assume $$x$$x is uniformly distributed between 0 and 2 minutes (0 to 120 seconds) part a: find the value of k and draw the corresponding density curve.
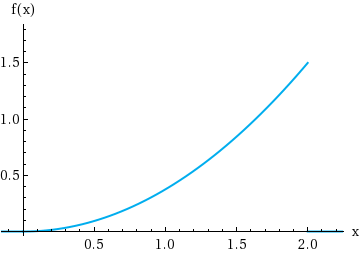
Solved A College Professor Never Finishes His Lecture Before The A college professor never finishes his lecture before the end of the hour and always finishes his lectures within \({\rm{2}}\) min after the hour. let \({\rm{x = }}\)the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of \({\rm{x}}\) is. College professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let x = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of x is as follows. f (x) = kx^2 0 ? x ? 2 (a) find the value of k. We can solve this problem by finding the probability that x, the time that elapses between the end of the hour and the end of the lecture, is between 60 and 90 seconds. since x is uniformly distributed between 0 and 120 seconds, we can find the probability by calculating the area under the probability density function (pdf) curve for x between. Question: a college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let x = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of x is as follows. f(x) = {kx² 0≤x≤2 otherwise (a) find the value of k.

Answered A College Professor Never Finishes His Bartleby We can solve this problem by finding the probability that x, the time that elapses between the end of the hour and the end of the lecture, is between 60 and 90 seconds. since x is uniformly distributed between 0 and 120 seconds, we can find the probability by calculating the area under the probability density function (pdf) curve for x between. Question: a college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let x = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of x is as follows. f(x) = {kx² 0≤x≤2 otherwise (a) find the value of k. A college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 minutes after the hour. let x be the time that elapses between the end of the hour and the end of the lecture, and suppose the pdf of x is as follows: f (x) = k x 2 0 ≤ x ≤ 2 (a) find the value of k. (enter your answer to. In our exercise, we deal with the continuous random variable \( x \), which represents the time in minutes after the hour when a professor might finish his lecture. the probability density function (pdf) for \( x \) is described by the equation:. A college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let x = x= x = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of x x x is. A college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. let \( x \) = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of \( x \) is as follows. \( f(x) = kx^2 \;\;\;\; 0 \le x \le 2 \;\;\;\; 0 \text{ otherwise}\) (a.
