Solved A F 0 B F 1 C F 2 D F 1 1 E F 1 2 F Chegg
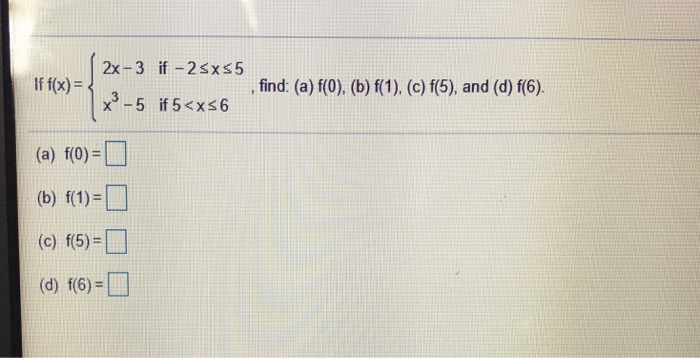
Solved Find A F 0 B F 1 C F 5 And D F 6 Chegg The kenya bankers association should monitor and supervise commercial banks in kenya to ensure financial reporting, legal and regulatory requirements are met by the banks and transparent periodic reporting to stakeholders on corporate governance, risk management and internal controls is undertaken. 5.4 limitations of the study the study was. Nairobi: kenya bankers association. olowa, o. w., &olowa, o. a. (2015).factors affecting entrepreneurship development in agribusiness enterprise in nyamira county, kenya. global journal of management and business research: b economics and commerce. olweny, t. (2012). the effect of monetary policy on private sector investment in kenya.
Answered A F 3 B F 2 C F 1 D F 0 E F 1 F F 2 Working paper series centre for research on financial markets and policy the centre for research on financial markets and policy® was established by the kenya bankers association in 2012 to ofer an array of research, commentary, and dialogue regarding critical policy matters that impact on financial markets in kenya. The data source is the 2016 finaccess household survey data which is both qualitative and quantitative collected collaboratively by central bank of kenya, kenya national bureau of statistics and financial sector deepening in 2015. a total of 8665 households were interviewed during the survey on access and usage of financial services in kenya [13] . In kenya, since 2015, the bank’s employees continue to decrease even with an increase in number of deposit accounts opened 1, 22. the dea model has been applied extensively in estimating efficiency in the banking sector. a study by 13 examined efficiency in the ethiopian commercial banks from 2011 2014. The wall street journal.
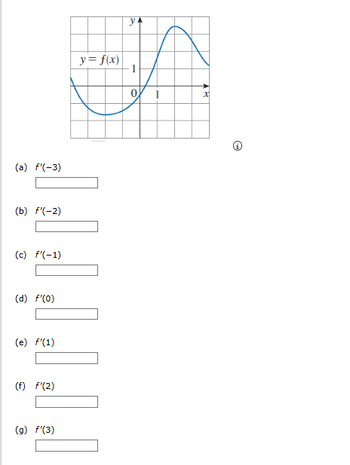
Answered A F 3 B F 2 C F 1 D Bartleby In kenya, since 2015, the bank’s employees continue to decrease even with an increase in number of deposit accounts opened 1, 22. the dea model has been applied extensively in estimating efficiency in the banking sector. a study by 13 examined efficiency in the ethiopian commercial banks from 2011 2014. The wall street journal. The role of capital requirements on bank competition and stability: the case of the kenyan banking industry; kba centre for research on financial markets and policy working paper 05; kenya bankers association (kba): nairobi, kenia, 2013. Kenya bankers association kba centre for research on financial markets and policy working paper series kamau a (2009) efficiency and productivity of the banking sector in kenya: an empirical investigation. Using the concept of structural power from business power theory (culpepper, 2015), we argue that, while recent efforts by the government have recognised the need to make digital credit less harmful through regulation, the market led ideology of the kenyan government combined with the structural power of banks and safaricom has limited the. I am a highly motivated, detail and results oriented economist working in the financial services sector. i am passionate about public policy, more specifically economic policy, public finance, labour economics and international development.

Solved 1 Find F 1 F 2 F 3 F 4 And F 5 If F Is Chegg The role of capital requirements on bank competition and stability: the case of the kenyan banking industry; kba centre for research on financial markets and policy working paper 05; kenya bankers association (kba): nairobi, kenia, 2013. Kenya bankers association kba centre for research on financial markets and policy working paper series kamau a (2009) efficiency and productivity of the banking sector in kenya: an empirical investigation. Using the concept of structural power from business power theory (culpepper, 2015), we argue that, while recent efforts by the government have recognised the need to make digital credit less harmful through regulation, the market led ideology of the kenyan government combined with the structural power of banks and safaricom has limited the. I am a highly motivated, detail and results oriented economist working in the financial services sector. i am passionate about public policy, more specifically economic policy, public finance, labour economics and international development.

Solved F 0 1 F 1 2 F 2 5 F N 3 2f N 2 F N 1 Chegg Using the concept of structural power from business power theory (culpepper, 2015), we argue that, while recent efforts by the government have recognised the need to make digital credit less harmful through regulation, the market led ideology of the kenyan government combined with the structural power of banks and safaricom has limited the. I am a highly motivated, detail and results oriented economist working in the financial services sector. i am passionate about public policy, more specifically economic policy, public finance, labour economics and international development.
Comments are closed.