
Solved Suppose A A B And B 1 2 3 Find A B 6 Chegg There are 2 steps to solve this one. (a) find a and b such that −3ai−(−1−i)b =3a−2bi. (b) let z1 = 12 5i and z2 = (3−2i)(2 λi). find λ without resorting to division such that z2 =z1. 3.2) let z= −2 3i and z′ = 5−4i. determine the complex numbers (a) z2−zz′ (b) 21(z−z ˉ)2. (c) 21[z−z ˉ] [(1 z ′)]2. not the question you’re looking for?. (a) find a and b such that −3ai − (−1 − i)b = 3a − 2bi. (b) let z 1 = 12 5i and z2 = (3 − 2i)(2 λi). find λ without resorting to division such that z 2 = z 1 .

Solved 3 Find If Possible A B A B 2a 2a B And B Chegg Answers #1 if $z {1}=a i b$ and $z {2}=c i d$ are two complex numbers such that $\left|z {1}\right|=\left|z {2}\right|=i$ and $\operatorname{re}\left(z {1} \bar{z} {2}\right)=0$, then the pair of complex numbers, $w {1}=a i c$ and $w {2}=b i d$ satisfy (a) $\left|w {1}\right|=1$ (b) $\left|w {2}\right|=1$ (c) $\left|w {1} \overrightarrow{w {2. To find a and b, we can equate the real and imaginary parts of both sides of the equation. the real part of ~3ai ( 1 i)b is b, and the real part of 3a 2bi is 3a. so we have b = 3a. Here’s the best way to solve it. express the complex equation − 3 a i − (− 1 − i) b = 3 a − 2 b i in terms of real and imaginary parts separately to find the values of a and b. a) a=b=0 b) … (3.1) (a) find a and b such that 3ai – ( 1 i)b = 3a 2bi. (b) let z1 = 12 5i and z2 = (3 21) (2 xi). 1. find a and b such that 3ai ( 1 i) b =3a 2bi; 2. let z=z1 z2 where z1=tantheta i and z2=z1. find an expression for zn with n e n; 3. explain how you will practice differentiations instruction when teaching about the topic of fraction; 4. find the eigenvalues and an eigenvector per eigenvalue of the matrix a= [ 0 1 1] [ 5. i.
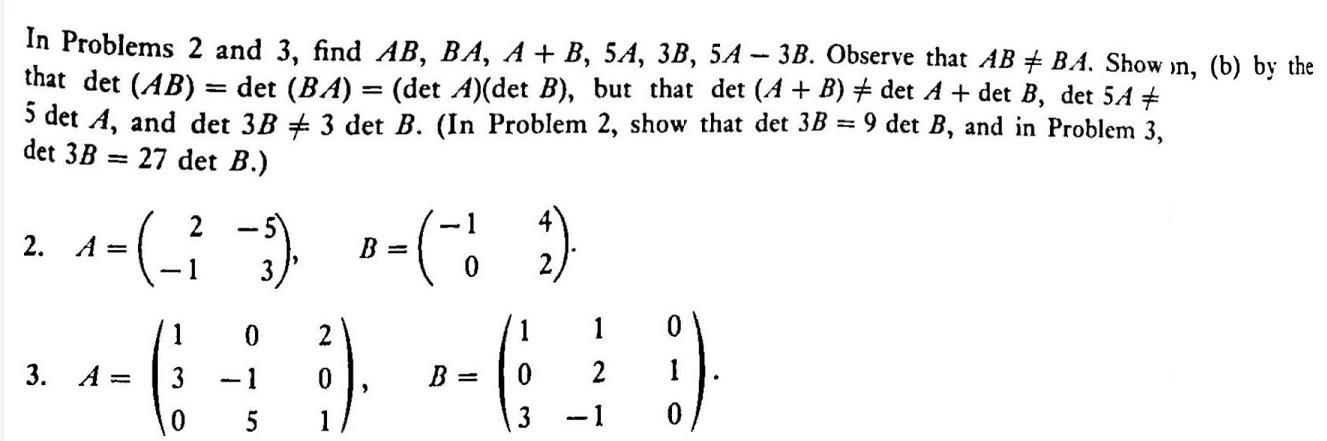
Solved In Problems 2 And 3 Find Ab Ba A B 5a 3b 5a 3b Chegg Here’s the best way to solve it. express the complex equation − 3 a i − (− 1 − i) b = 3 a − 2 b i in terms of real and imaginary parts separately to find the values of a and b. a) a=b=0 b) … (3.1) (a) find a and b such that 3ai – ( 1 i)b = 3a 2bi. (b) let z1 = 12 5i and z2 = (3 21) (2 xi). 1. find a and b such that 3ai ( 1 i) b =3a 2bi; 2. let z=z1 z2 where z1=tantheta i and z2=z1. find an expression for zn with n e n; 3. explain how you will practice differentiations instruction when teaching about the topic of fraction; 4. find the eigenvalues and an eigenvector per eigenvalue of the matrix a= [ 0 1 1] [ 5. i. Texts: question 3: 5 marks (3.1) a) find a and b such that 3ai ( 1 ib) = 3a 2bi. (1) b) let z = 12 5i and z2 = 3 2i^2 x. find x without resorting to division such that z^2 = z1. (1) (3.2) let z = 2 3i and z' = 5 4i. determine the complex numbers: a) az^2 zz. (1) b) bz z. z[z ] [z z]{( (1) (1). Solve part (3.1)(a) given equation: \[ 3ai ( 1 ib) = 3a 2bi \] first, simplify the left hand side: \[ 3ai 1 ib = 3a 2bi \] separate the real and imaginary parts: real part: \( 1 = 3a \) imaginary part: \( 3a b = 2b \) from the real part: \[ 1 = 3a \] \[ a = \frac{1}{3} \] from the imaginary part: \[ 3a b = 2b \] \[ b = 2b. There are 4 steps to solve this one. (a) find a and b such that −3ai−(−1−i)b =3a−2bi. (b) let z1 = 12 5i and z2 = (3−2i)(2 λi). find λ without resorting to division such that z 2 = z 1 2) let z= −2 3i and z′ = 5−4i. determine the complex numbers (a) z2−zz′ (b) 21(z zˉ)2 (c) 21[z−zˉ] [(−1−z′)]2. not the question you’re looking for?. Let us find "a" and "b" such that " 3ai ( 1 i) b =3a 2bi." it follows that " 3ai b bi =3a 2bi," and hence "b (b 3a)i =3a 2bi". taking into account that two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal, we conclude that "b=3a, b 3a = 2b." then "b=3a" and "3b=3a.".

Solved In Problems 2 And 3 Find Ab Ba A B 5a 3b 5a 3b Chegg Texts: question 3: 5 marks (3.1) a) find a and b such that 3ai ( 1 ib) = 3a 2bi. (1) b) let z = 12 5i and z2 = 3 2i^2 x. find x without resorting to division such that z^2 = z1. (1) (3.2) let z = 2 3i and z' = 5 4i. determine the complex numbers: a) az^2 zz. (1) b) bz z. z[z ] [z z]{( (1) (1). Solve part (3.1)(a) given equation: \[ 3ai ( 1 ib) = 3a 2bi \] first, simplify the left hand side: \[ 3ai 1 ib = 3a 2bi \] separate the real and imaginary parts: real part: \( 1 = 3a \) imaginary part: \( 3a b = 2b \) from the real part: \[ 1 = 3a \] \[ a = \frac{1}{3} \] from the imaginary part: \[ 3a b = 2b \] \[ b = 2b. There are 4 steps to solve this one. (a) find a and b such that −3ai−(−1−i)b =3a−2bi. (b) let z1 = 12 5i and z2 = (3−2i)(2 λi). find λ without resorting to division such that z 2 = z 1 2) let z= −2 3i and z′ = 5−4i. determine the complex numbers (a) z2−zz′ (b) 21(z zˉ)2 (c) 21[z−zˉ] [(−1−z′)]2. not the question you’re looking for?. Let us find "a" and "b" such that " 3ai ( 1 i) b =3a 2bi." it follows that " 3ai b bi =3a 2bi," and hence "b (b 3a)i =3a 2bi". taking into account that two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal, we conclude that "b=3a, b 3a = 2b." then "b=3a" and "3b=3a.".
