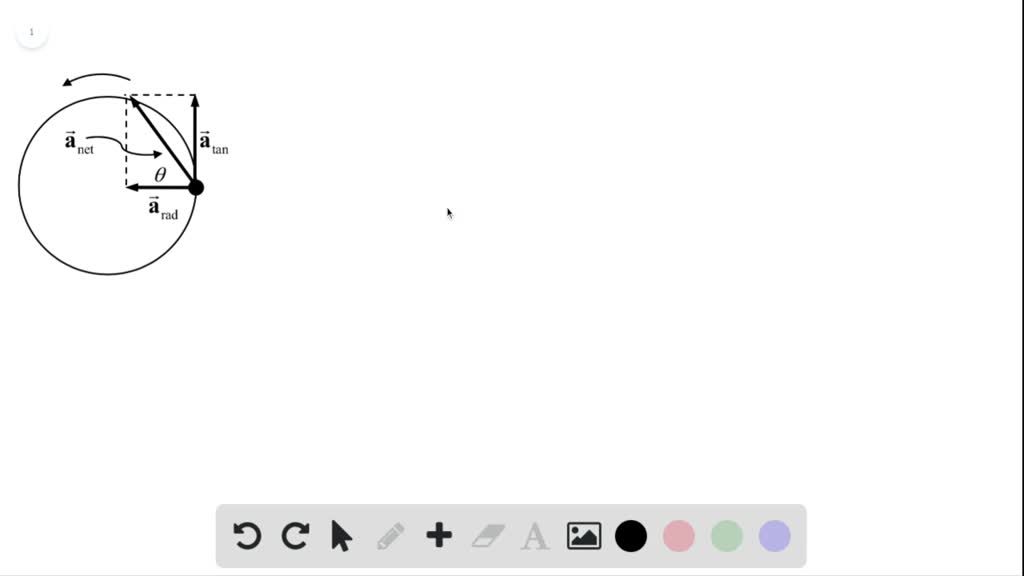
Solved Iii A Hammer Thrower Accelerates The Hammer Mass 7 30 Kg In a track and field event, a hammer thrower accelerates the hammer (mass = 7.30 kg) from rest within four full turns (revolutions) and releases it at a speed of 22.0 m s. assuming a uniform rate of increase in angular velocity and a radius of 1.30 m, calculate the angular acceleration. Answer of a hammer thrower accelerates the hammer (mass = 7.10 kg) from rest within four full turns (revolutions) and releases i | solutioninn.

Solved A Hammer Thrower Accelerates The Hammer Solutioninn In the case of the hammer thrower, the hammer accelerates uniformly, and we use the formula for angular acceleration, \( \alpha \), which is given by: \( \alpha = \frac{\omega^2}{2\theta} \) here, \( \omega \) represents the final angular speed, and \( \theta \) is the angular displacement. A hammer thrower accelerates the hammer from rest in four complete rotations (revolutions) and releases it with a speed of 26.5 m s, then the angular acceleration is α = (0 − 26.5 1.20) [(4 × 2 π × 1.20) 26.5] to solve this problem, we'll use the following equations: (a) angular acceleration (α) can be calculated using the formula: α. Calculate the centripetal acceleration just before release. calculate the net force being exerted on the hammer by the athlete just before release. ignore gravity. calculate the angle of this force with respect to the radius of the circular motion. here’s the best way to solve it. to solve this problem, we need to use the relation. A hammer thrower accelerates the hammer (mass = 7.30kg) from rest within four full turns (revolution) and releases it at a speed of 28.0m s. assuming a uniform rate of increase in angular velocity.
Solved Iii A Hammer Thrower Accelerates The Hammer Mass 7 30 Kg Calculate the centripetal acceleration just before release. calculate the net force being exerted on the hammer by the athlete just before release. ignore gravity. calculate the angle of this force with respect to the radius of the circular motion. here’s the best way to solve it. to solve this problem, we need to use the relation. A hammer thrower accelerates the hammer (mass = 7.30kg) from rest within four full turns (revolution) and releases it at a speed of 28.0m s. assuming a uniform rate of increase in angular velocity. A hammer thrower accelerates the hammer (mass = 7.3 kg) from rest within four full turns (revolutions) and releases it at a speed of 27.2 m s. Answer of a hammer thrower accelerates the hammer (mass = 7.30kg) from rest within four full turns (revolution) and releases it | solutioninn all matches solution library. A hammer thrower accelerates the hammer (mass = 7.30 kg) from rest within four full turns (revolutions) and releases it at a speed of 26.5 m s. assuming a uniform rate of increase in angular velocity and a horizontal circular path of radius 1.20 m, calculate the angular acceleration, the (linear) tangential acceleration,. (iii) a hammer thrower accelerates the hammer of mass 7.30 kg (fig. 10 64 므) from rest within four full turns (revolutions) and releases it at a speed of 26.5 m s. assuming a uniform rate of increase in angular velocity and a horizontal circular path of radius 1.20 m, calculate (a) the angular acceleration, (b) the (linear) tangential.
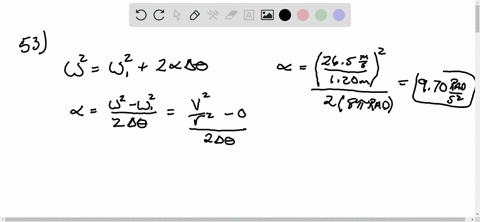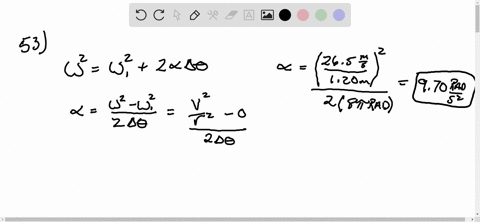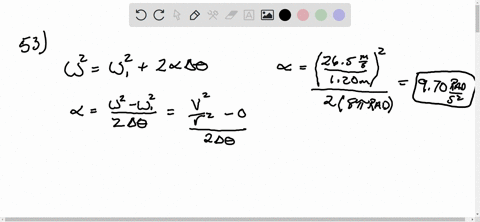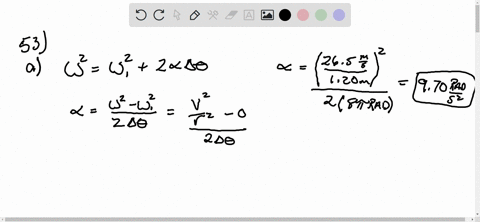
Solved A Hammer Thrower Accelerates The Hammer Mass 7 30 Kg From A hammer thrower accelerates the hammer (mass = 7.3 kg) from rest within four full turns (revolutions) and releases it at a speed of 27.2 m s. Answer of a hammer thrower accelerates the hammer (mass = 7.30kg) from rest within four full turns (revolution) and releases it | solutioninn all matches solution library. A hammer thrower accelerates the hammer (mass = 7.30 kg) from rest within four full turns (revolutions) and releases it at a speed of 26.5 m s. assuming a uniform rate of increase in angular velocity and a horizontal circular path of radius 1.20 m, calculate the angular acceleration, the (linear) tangential acceleration,. (iii) a hammer thrower accelerates the hammer of mass 7.30 kg (fig. 10 64 므) from rest within four full turns (revolutions) and releases it at a speed of 26.5 m s. assuming a uniform rate of increase in angular velocity and a horizontal circular path of radius 1.20 m, calculate (a) the angular acceleration, (b) the (linear) tangential.
