
Solved 1 Let U1 2 0 2 1 U2 1 2 0 2 And U3 1 1 0 1 Chegg Given vectors u = (3, 1, 2), v 1 = (1, 0, − 1), v 2 = (2, 1, 3), v 3 = (4, 2, 6) u = c 1 v 1 c 2 v 2 c 3 v 3. (a) let u= (3,1,2),v1 = (1,0,−1),v2 = (2,1,3),v3 = (4,2,6). find c1,c2,c3 such that u= c1v1 c2v2 c3v3. (b) find the coordinate vector of u= (2,−1,1) relative to the basis s ={v1,v2,v3} with v1 =(1,1,0),v2 =(1,0,1),v3 =(0,1,1). Let a = [ 3 1 2 6 2 4 1 2 5 1 3 8], w = [1 1 2 1] and v = [ 1 0 2]. (1) determine if w is in nul a. (2) determine if v is in col a. (3) find bases of nul a and col a. let b 1 = [1 2 3], b 2 = [5 0 2], b 3. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.

Let U1 1 1 1 1 U2 1 2 1 2 U3 1 3 0 Chegg Below i've provided a few methods of determining whether or not they are linearly independent. method #1. ⎡⎣⎢1 1 2 1 0 1 2 2 3⎤⎦⎥ [1 1 2 1 0 2 2 1 3] now use gauss jordan elimination to determine the rank of the matrix. if it is 3 3 (the number of columns), then the columns are linearly independent. method #2. construct the same matrix as above. V(u). exercise 6.1.5 (ex. 4, p. 371) let t(v1,v2,v3) = (2v1 v2,2v2 −3v1,v1 −v3) 1. compute t(−4,5,1). solution: t(−4,5,1) = (2∗(−4) 5,2∗5−3∗(−4),−4−1) = (−3,22,−5). 2. compute the preimage of w = (4,1,−1). solution: suppose (v1,v2,v3) is in the preimage of (4,1,−1). then (2v1 v2,2v2 −3v1,v1 −v3) = (4,1,−1. Let u = (3, 1, 2), v 1 = (1, 0, − 1), v 2 = (2, 1, 3), v 3 = (4, 2, 6). find c 1 , c 2 , c 3 such that u = c 1 v 1 c 2 v 2 c 3 v 3 . not the question you’re looking for?. You'll get a detailed solution from a subject matter expert that helps you learn core concepts. ' let v 1 = [1 0 1], v 2 = [2 1 3], v 3 = [4 2 6], and w = [3 1 2]. a. is w in {v 1, v 2, v 3s}? how many vectors are in {v 1, v 2, v 3s}? b. how many vectors are in span {v 1, v 2, v 3s}? c. is w in the subspace spanned by {v 1, v 2, v 3s}? why?'.
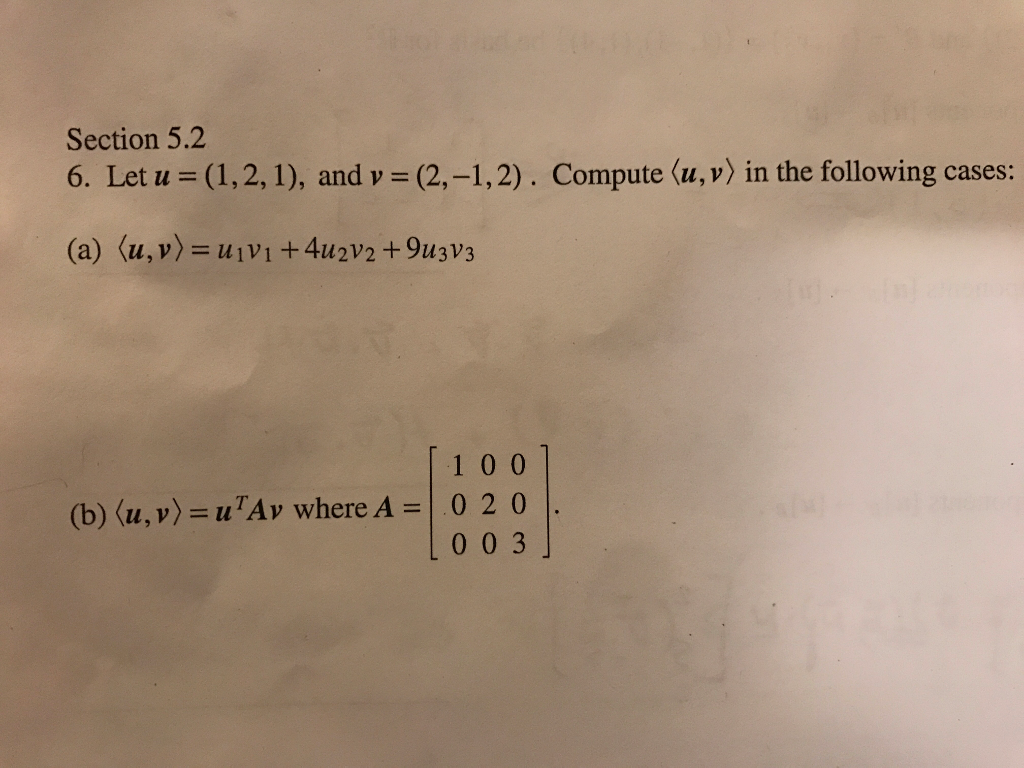
Solved Let U 1 2 1 And V 2 1 2 Compute U V Chegg Let u = (3, 1, 2), v 1 = (1, 0, − 1), v 2 = (2, 1, 3), v 3 = (4, 2, 6). find c 1 , c 2 , c 3 such that u = c 1 v 1 c 2 v 2 c 3 v 3 . not the question you’re looking for?. You'll get a detailed solution from a subject matter expert that helps you learn core concepts. ' let v 1 = [1 0 1], v 2 = [2 1 3], v 3 = [4 2 6], and w = [3 1 2]. a. is w in {v 1, v 2, v 3s}? how many vectors are in {v 1, v 2, v 3s}? b. how many vectors are in span {v 1, v 2, v 3s}? c. is w in the subspace spanned by {v 1, v 2, v 3s}? why?'. Answer to 4. let u = (3, 1, 2), v1 = (1, 0, 1), v2 (2, 1,3), v3 = (4, answered step by step. solved by verified expert. A) find the transition matrix from the ordered basis {v1, v2, v3} to the ordered basis {u1, u2, u3}. b) if x = 2v1 3v2 − 4v3, determine the coordinates of x with respect to {u1, u2, u3}. let u1 =(1,1,1)^t,u2 =(1,2,2)^t, and u3 =(2,3,4)^t and v1 =(4,6,7)^t,v2 =(0,1,1)^t, and. Let v 1, v 2,…, v r be vectors in r n. a linear combination of these vectors is any expression of the form where the coefficients k 1, k 2,…, k r are scalars. example 1: the vector v = (−7, −6) is a linear combination of the vectors v 1 = (−2, 3) and v 2 = (1, 4), since v = 2 v 1 − 3 v 2. The answer is yes, w is in the subspace spanned by {v1, v2, v3}. to check if w is in the subspace spanned by {v1, v2, v3}, we need to see if w can be written as a linear combination of v1, v2, and v3. that is, we need to check if there exist scalars a, b, and c such that aw bv1 cv2 = w. solving the system of equations:.

Let U1 1 1 1 1 U2 1 2 1 2 U3 1 3 0 Chegg Answer to 4. let u = (3, 1, 2), v1 = (1, 0, 1), v2 (2, 1,3), v3 = (4, answered step by step. solved by verified expert. A) find the transition matrix from the ordered basis {v1, v2, v3} to the ordered basis {u1, u2, u3}. b) if x = 2v1 3v2 − 4v3, determine the coordinates of x with respect to {u1, u2, u3}. let u1 =(1,1,1)^t,u2 =(1,2,2)^t, and u3 =(2,3,4)^t and v1 =(4,6,7)^t,v2 =(0,1,1)^t, and. Let v 1, v 2,…, v r be vectors in r n. a linear combination of these vectors is any expression of the form where the coefficients k 1, k 2,…, k r are scalars. example 1: the vector v = (−7, −6) is a linear combination of the vectors v 1 = (−2, 3) and v 2 = (1, 4), since v = 2 v 1 − 3 v 2. The answer is yes, w is in the subspace spanned by {v1, v2, v3}. to check if w is in the subspace spanned by {v1, v2, v3}, we need to see if w can be written as a linear combination of v1, v2, and v3. that is, we need to check if there exist scalars a, b, and c such that aw bv1 cv2 = w. solving the system of equations:.
