
Solved Prove That 1 X X2 Xn 1 1 Xn 1 X Chegg (a) prove that if x =1, then 1 x x2 ⋯ xn=1−x1−xn 1 (b) use (a) to prove that if ∣x∣<1, then limn→∞ (∑j=0nxj)=1−x1. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Simply multiplying all the terms by $x^1$ increases the exponents of $x$ by $1$ in each term. so $x^n\cdot x^1=x^{n 1}.$.
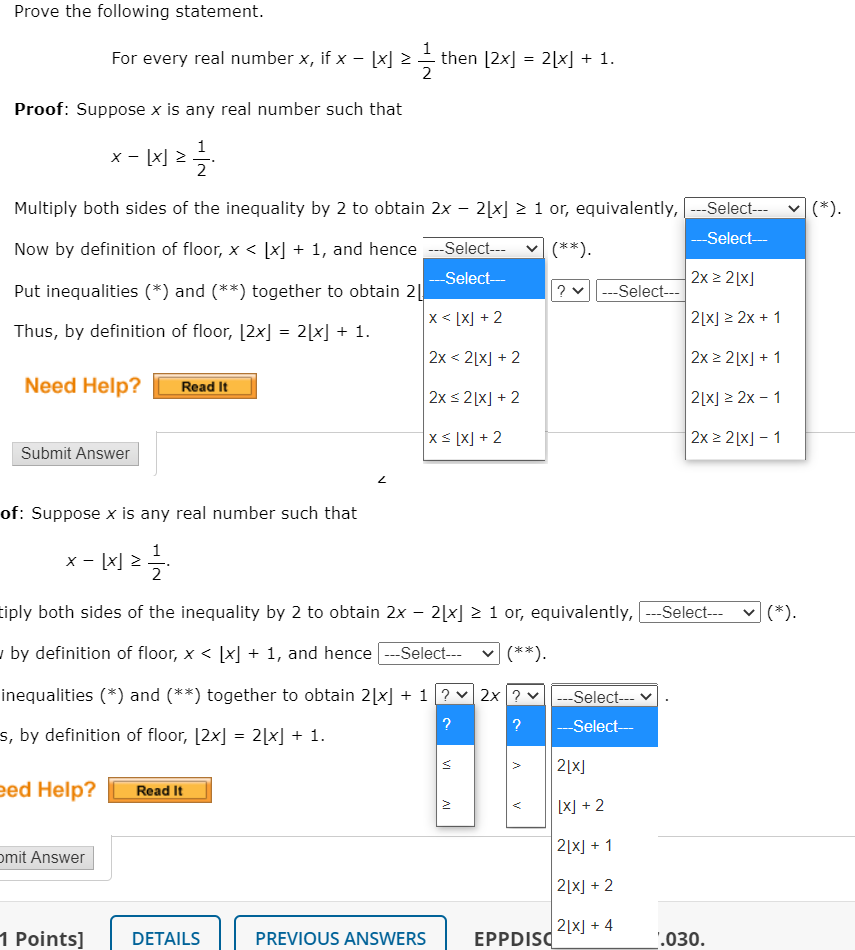
Solved Prove The Following Statement For Every Real Number Chegg "use mathematical induction to prove that if x > 1, then ( (1 x)^2 ) >= 1 nx". you have miswritten the problem. this is the bernoulli inequality: we have proven for n = 1, assumed for n = k, and proved for n = k 1, so our induction proof is complete. nicely worked out !!! still looking for help? get the right answer, fast. Free math problem solver answers your algebra homework questions with step by step explanations. I am thinking that x^2>1 is x*x>1, if divided by x then x>1. and that x*x must produce a positive number. but im not sure how to use this for a direct proof or a contradiction. i need to be able to show both proofs. Differentiate the function with respect to x. prove that the function f given by f (x) = | x 1 |, x ∈ r is not differentiable at x = 1. if (x – a) 2 (y – b) 2 = c 2, for some c > 0, prove that [1 (d y d x) 2] 3 2 d 2 y d x 2 is a constant independent of a and b. differential coefficient of sec (tan –1 x) w.r.t. x is .

Solved 1 Prove Or Disprove The Following Statements A If Chegg I am thinking that x^2>1 is x*x>1, if divided by x then x>1. and that x*x must produce a positive number. but im not sure how to use this for a direct proof or a contradiction. i need to be able to show both proofs. Differentiate the function with respect to x. prove that the function f given by f (x) = | x 1 |, x ∈ r is not differentiable at x = 1. if (x – a) 2 (y – b) 2 = c 2, for some c > 0, prove that [1 (d y d x) 2] 3 2 d 2 y d x 2 is a constant independent of a and b. differential coefficient of sec (tan –1 x) w.r.t. x is . ⇒ x 1 x = 2. let x = 1, then condition satisfied. ⇒ x 2 1 x 2. put x = 1. ⇒ 1 1. ⇒ 2. detailed method: ⇒ x 1 x = 2. as we know, ⇒ x 2 1 x 2 = (x 1 x) 2 – 2. ⇒ x 2 1 x 2 = 2 2 – 2 = 4 – 2 = 2. Video answer: we need to prove that the x plus one over banks was better. you prove this one. let's look at the angst. half minus expo. we are aware of this grand. the difference was scrambled. we're always great. you get an extra half square minus. To prove that (1 x) (1 x 2) (1 x 4) (1 x 8) (1 x 16) = (1 − x) (1 − x 32), we will expand the left hand side and simplify it to match the right hand side. step by step solution: step 1. start with the left hand side: (1 x) (1 x 2) (1 x 4) (1 x 8) (1 x 16). step 2. notice that each factor can be rewritten as a sum of. If $x^2 = 1$, then $x^2 1 = 0$, so $(x 1)(x 1) = 0$. because fields are integral domains, either $x 1 = 0$ or $x 1 = 0$ , and the question is solved as you claim. this is a specific instance of lulu's comment that fields can have at most $d$ solutions to a polynomial of degree $d$ .

Let X1 X2 Xn N 1 Be Iid Random Variables Having The Normal ⇒ x 1 x = 2. let x = 1, then condition satisfied. ⇒ x 2 1 x 2. put x = 1. ⇒ 1 1. ⇒ 2. detailed method: ⇒ x 1 x = 2. as we know, ⇒ x 2 1 x 2 = (x 1 x) 2 – 2. ⇒ x 2 1 x 2 = 2 2 – 2 = 4 – 2 = 2. Video answer: we need to prove that the x plus one over banks was better. you prove this one. let's look at the angst. half minus expo. we are aware of this grand. the difference was scrambled. we're always great. you get an extra half square minus. To prove that (1 x) (1 x 2) (1 x 4) (1 x 8) (1 x 16) = (1 − x) (1 − x 32), we will expand the left hand side and simplify it to match the right hand side. step by step solution: step 1. start with the left hand side: (1 x) (1 x 2) (1 x 4) (1 x 8) (1 x 16). step 2. notice that each factor can be rewritten as a sum of. If $x^2 = 1$, then $x^2 1 = 0$, so $(x 1)(x 1) = 0$. because fields are integral domains, either $x 1 = 0$ or $x 1 = 0$ , and the question is solved as you claim. this is a specific instance of lulu's comment that fields can have at most $d$ solutions to a polynomial of degree $d$ .
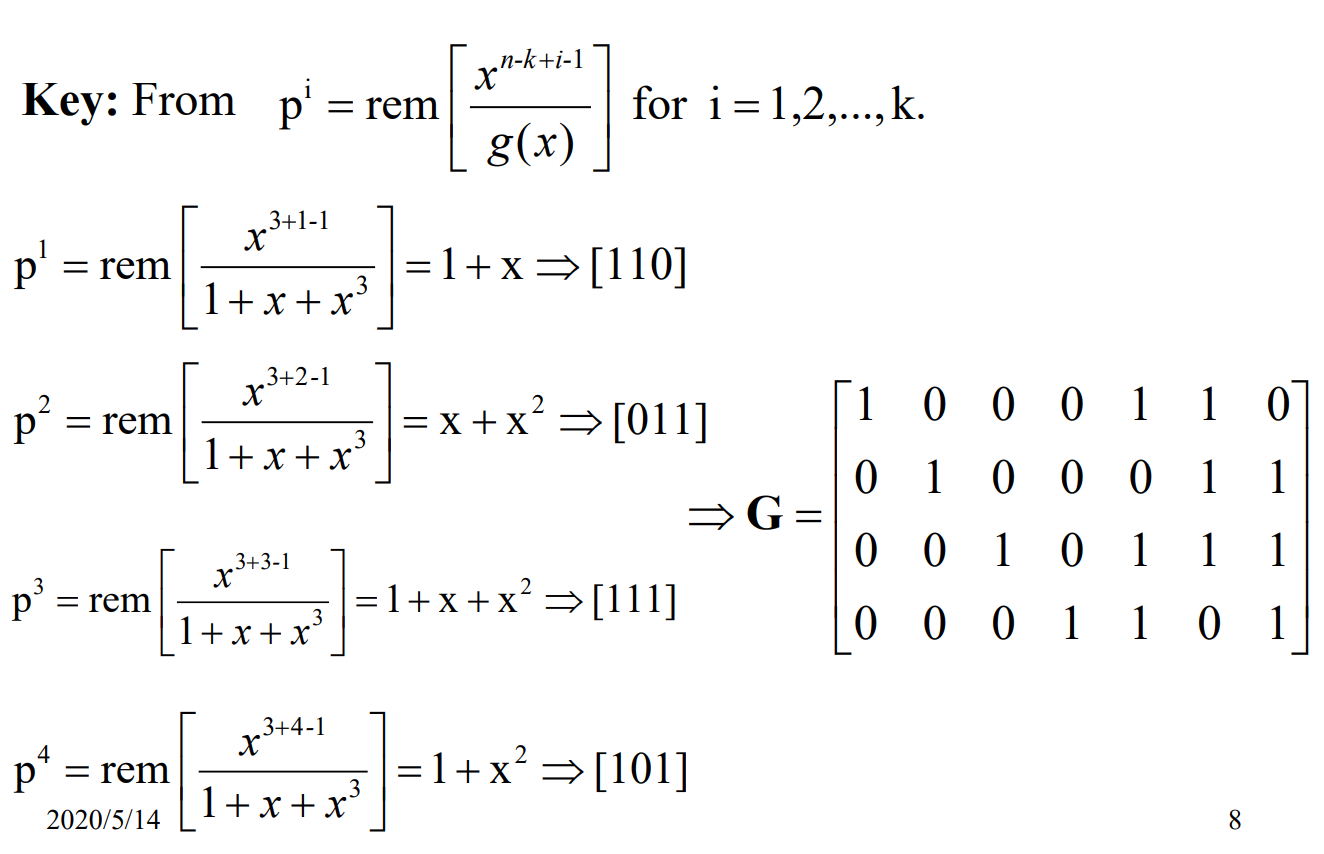
Find Generator Matrix Of Linear Block Code If Code Chegg To prove that (1 x) (1 x 2) (1 x 4) (1 x 8) (1 x 16) = (1 − x) (1 − x 32), we will expand the left hand side and simplify it to match the right hand side. step by step solution: step 1. start with the left hand side: (1 x) (1 x 2) (1 x 4) (1 x 8) (1 x 16). step 2. notice that each factor can be rewritten as a sum of. If $x^2 = 1$, then $x^2 1 = 0$, so $(x 1)(x 1) = 0$. because fields are integral domains, either $x 1 = 0$ or $x 1 = 0$ , and the question is solved as you claim. this is a specific instance of lulu's comment that fields can have at most $d$ solutions to a polynomial of degree $d$ .
