
Solved A Show That The Symmetric Group Sn Has Only Two Chegg Question: (a) show that the symmetric group sn has only two 1 dimensional representations. (hint:consider a 1 dimensional representation. what are the possible values of the representation for a particular transposition? are all transpositions represented by the same number or by different numbers?). Consider the symmetric group sn, with n≥3. the goal of this problem is to prove that sn can be generated by only two elements. (a) let τ∈sn be a permutation, and (ab) be a transposition. show that τ (ab)τ−1= (τ (a)τ (b) ), the transposition changing τ (a) and τ (b). (b) show that (ij) = ( 1i) ( 1j) ( 1i).

Solved 2 The Symmetric Group Sn And The Sign Homomorphism Chegg The better answer is probably the accepted one: the sign homomorphism is the only non trivial homomorphism ϕ: sn → {±1} ϕ: s n → {± 1}. this uniquely identifies an a n as the only index 2 subgroup of sn s n. In this page, we will prove that the symmetric group s n is not commutative. before that let us recall abelian group. a group (g, ∗) is called an abelian group if a∗b = b∗a ∀ a,b ∈ g, that is, the elements of g commute each other. let us prove that the symmetric group s n is not abelian whenever n≥3. Proof. as we have seen, every σ ∈ s. determines a partition of {1, , n} into orbits under the action of (σ). if σ ≠ e, then (σ) has nontrivial orbits. as σ acts as a cycle on each orbit, it follows that σ may be written as a product of cycles. the proof of the uniqueness is left to the reader (exercise 4.2). Consider the symmetric group sn, with n > 3. the goal of this problem is to prove that sn can be generated by only two elements. (a) let te sn be a permutation, and (ab) be a transposition. show that t (ab)7 1 (7 (a) 7 (b)), the transposition changing t (a) and 7 (b). (b) show that (ij) = (11) (1j) (li).
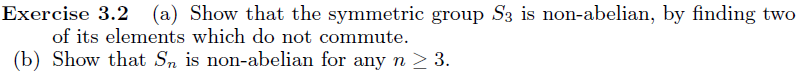
Solved Exercise 3 2 A Show That The Symmetric Group S3 Is Chegg Proof. as we have seen, every σ ∈ s. determines a partition of {1, , n} into orbits under the action of (σ). if σ ≠ e, then (σ) has nontrivial orbits. as σ acts as a cycle on each orbit, it follows that σ may be written as a product of cycles. the proof of the uniqueness is left to the reader (exercise 4.2). Consider the symmetric group sn, with n > 3. the goal of this problem is to prove that sn can be generated by only two elements. (a) let te sn be a permutation, and (ab) be a transposition. show that t (ab)7 1 (7 (a) 7 (b)), the transposition changing t (a) and 7 (b). (b) show that (ij) = (11) (1j) (li).
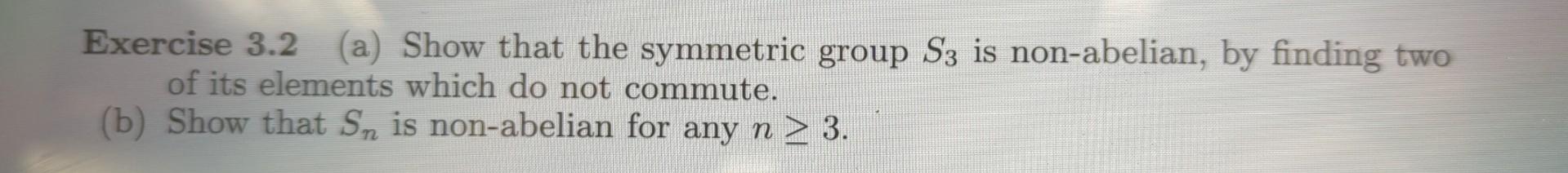
Solved Exercise 3 2 A Show That The Symmetric Group S3 Is Chegg
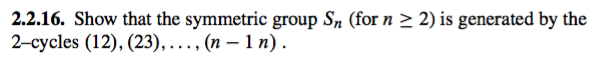
Solved 2 2 16 Show That The Symmetric Group Sn For N 2 2 Chegg
