
Solved Absolute Conditional Convergence Ratio Test Power Chegg Answer to solved absolute conditional convergence, ratio test, power | chegg. Our expert help has broken down your problem into an easy to learn solution you can count on. question: absolute conditional convergence problem (9pts) determine whether the following series are absolutely convergent, conditionally convergent, or divergent. (6) ¿ cos (7m) 1 is ?.

Solved 1 Absolute Convergence Conditional Convergence Chegg In this section we will discuss using the ratio test to determine if an infinite series converges absolutely or diverges. the ratio test can be used on any series, but unfortunately will not always yield a conclusive answer as to whether a series will converge absolutely or diverge. Root and ratio tests the ratio test is a convergence test that can be particularly helpful when the series at hand has terms involving factorials or nth powers: ratio test. let p a n be a series so that lim n!1 a n 1 a n = ˆ: 1.if ˆ>1 or ˆ= 1, the series p a n diverges. 2.if ˆ<1, the series p a n converges absolutely (i.e., p a n and p ja. The ratio test this test is useful for determining absolute convergence. let p 1 n=1 a n be a series (the terms may be positive or negative). let l= lim n!1 a n 1 an . if l<1, then the series p 1 n=1 a n converges absolutely (and hence is convergent). if l>1 or 1, then the series p 1 n=1 a n is divergent. if l= 1, then the ratio test is. • to find the radius of convergence, we apply ratio test for absolute convergence of the power series • to find the interval of convergence, investigate the convergence at the endpoints |𝑥−𝑎|= example: plot the partial sums of σ𝑛=1 ∞ 𝑥𝑛.
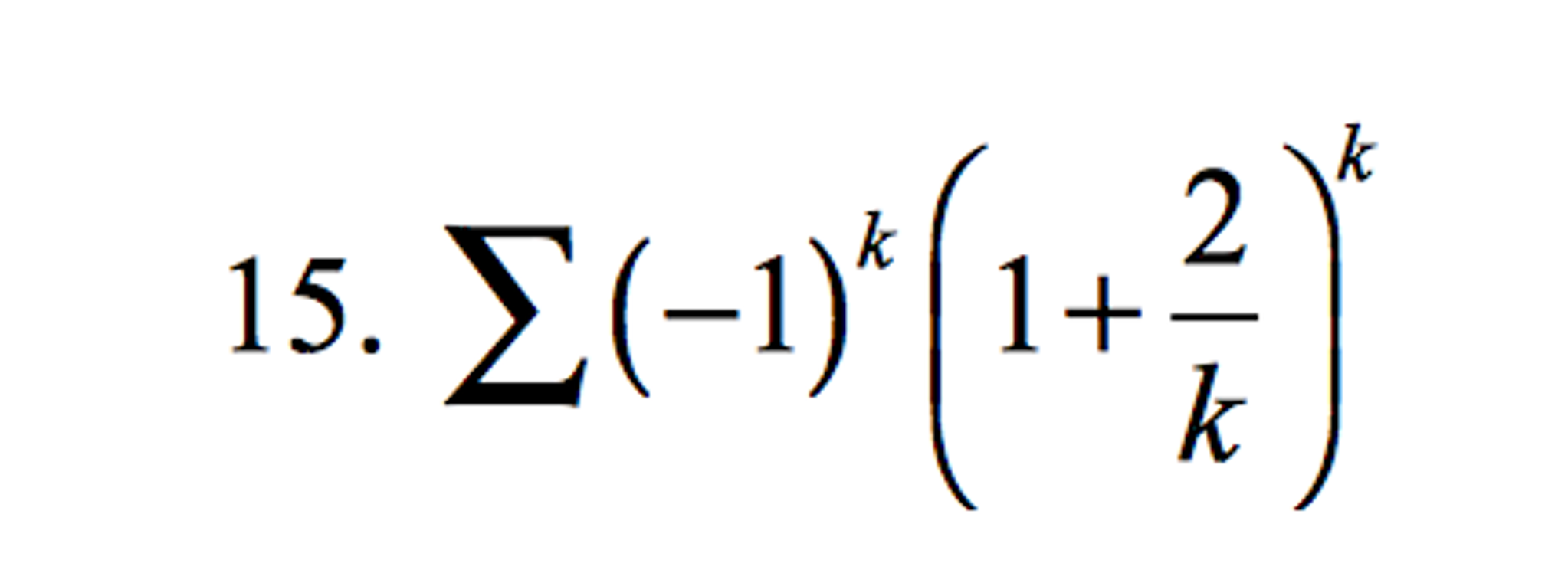
Solved 2 Chegg The ratio test this test is useful for determining absolute convergence. let p 1 n=1 a n be a series (the terms may be positive or negative). let l= lim n!1 a n 1 an . if l<1, then the series p 1 n=1 a n converges absolutely (and hence is convergent). if l>1 or 1, then the series p 1 n=1 a n is divergent. if l= 1, then the ratio test is. • to find the radius of convergence, we apply ratio test for absolute convergence of the power series • to find the interval of convergence, investigate the convergence at the endpoints |𝑥−𝑎|= example: plot the partial sums of σ𝑛=1 ∞ 𝑥𝑛. Ratio test theorem (ratio test) given x∞ k=1 ak, with ak ̸= 0 for all k, suppose that lim k→∞ ak 1 ak = l. then 1. if l <1, the series converges absolutely, 2. if l >1, the series diverges, 3. if l = 1, there is no conclusion. Question: se to show absolute convergence, conditional convergence, or divergence [10 pts): use the ratio test to help find 1) the radius of convergence and 2) the interval of convergence of the following power series. The ratio test is very useful for determining values of a variable which guarantee the absolute convergence (and convergence) of a series. this is a method we will use often in the rest of this chapter. Here’s the best way to solve it. 1. absolute convergence, conditional convergence, divergence: use any test, including root or ratio test a. determine the convergence # 15, 10, 18, 20 3" ( 3)" 9. Σ ( 1) 1 10. Σ 2"n (2n 1)! n=1 x=0 11. Σ 1 k!.

Solved 3 Test The Following For Absolute Convergence Chegg Ratio test theorem (ratio test) given x∞ k=1 ak, with ak ̸= 0 for all k, suppose that lim k→∞ ak 1 ak = l. then 1. if l <1, the series converges absolutely, 2. if l >1, the series diverges, 3. if l = 1, there is no conclusion. Question: se to show absolute convergence, conditional convergence, or divergence [10 pts): use the ratio test to help find 1) the radius of convergence and 2) the interval of convergence of the following power series. The ratio test is very useful for determining values of a variable which guarantee the absolute convergence (and convergence) of a series. this is a method we will use often in the rest of this chapter. Here’s the best way to solve it. 1. absolute convergence, conditional convergence, divergence: use any test, including root or ratio test a. determine the convergence # 15, 10, 18, 20 3" ( 3)" 9. Σ ( 1) 1 10. Σ 2"n (2n 1)! n=1 x=0 11. Σ 1 k!.

Solved Problem 1 Test The Series For Absolute Convergence Chegg The ratio test is very useful for determining values of a variable which guarantee the absolute convergence (and convergence) of a series. this is a method we will use often in the rest of this chapter. Here’s the best way to solve it. 1. absolute convergence, conditional convergence, divergence: use any test, including root or ratio test a. determine the convergence # 15, 10, 18, 20 3" ( 3)" 9. Σ ( 1) 1 10. Σ 2"n (2n 1)! n=1 x=0 11. Σ 1 k!.
