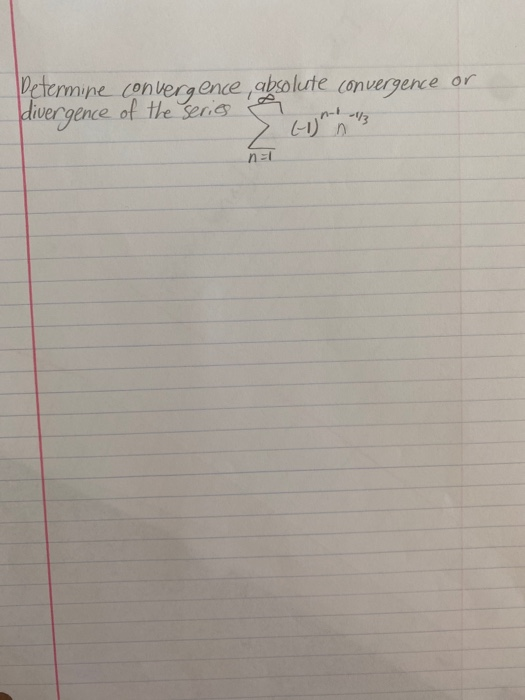
Solved Determine Convergence Absolute Convergence Or Chegg For each series, determine what information, if any, the ratio test gives. nº a) Σ n! η = 0 n b) Σ η 1 η = Ο c)Σ n! 10" η = 0. there are 2 steps to solve this one. to determine what information the ratio test provides for each of the given series, we'll apply the absolute convergence. For each of the following series determine if they are absolutely convergent, conditionally convergent or divergent. here is a set of practice problems to accompany the absolute convergence section of the series & sequences chapter of the notes for paul dawkins calculus ii course at lamar university.
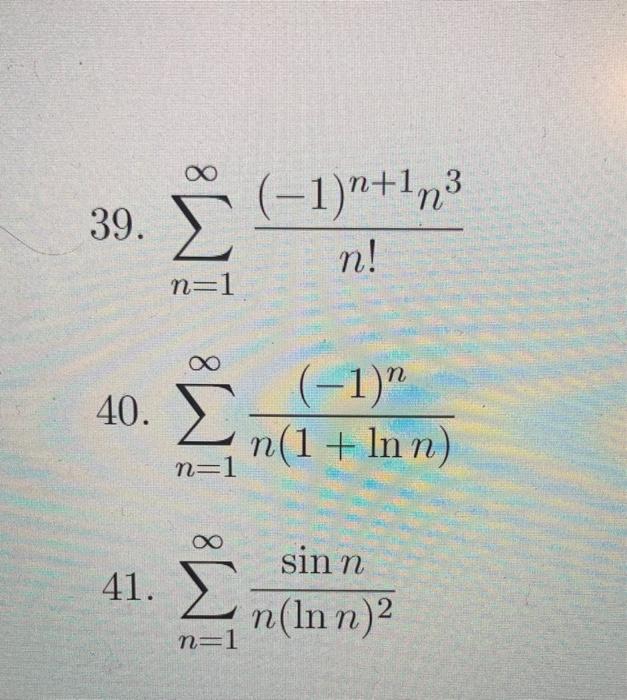
Solved Determine Either Absolute Convergence Conditional Chegg Determine if the series converges absolutely, converges conditionally, or diverges. find the exact value for the sum of the convergent series. $$1 \frac{1}{5} \frac{1}{5^2} \frac{1}{5^3} \frac{1}{5^4} \frac{1}{5^5} \frac{1}{5^6} \frac{1}{5^7} \frac{1}{5^8} $$ i have no clue where to start. Example \(\pageindex{3}\): determining absolute and conditional convergence. determine if the following series converge absolutely, conditionally, or diverge. 1.\( \sum\limits {n=1}^\infty ( 1)^n\dfrac{n 3}{n^2 2n 5}\qquad 2. \sum\limits {n=1}^\infty ( 1)^n\dfrac{n^2 2n 5}{2^n}\qquad 3.\sum\limits {n=3}^\infty ( 1)^n\dfrac{3n 3}{5n 10}\) solution. Absolute convergence. for each series, determine what information, if any, the root or ratio test gives. show the details of your limit computation. Absolute convergence. if the series \( \sum {n}u {n}\) converges, with \(\sum {n}\left | u {n} \right |\) signifying the absolute value, then the series \(\left | u {n} \right |\) is said to converge absolutely. in addition, if a series is multiplied by another absolutely convergent series, the product series will also converge absolutely.
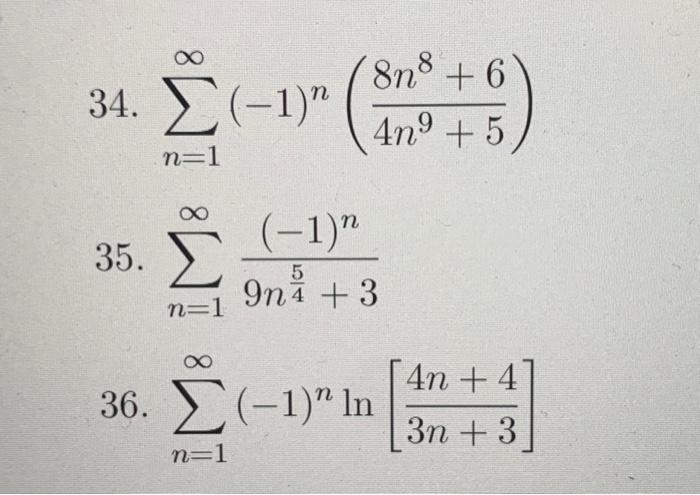
Solved Determine Either Absolute Convergence Conditional Chegg Absolute convergence. for each series, determine what information, if any, the root or ratio test gives. show the details of your limit computation. Absolute convergence. if the series \( \sum {n}u {n}\) converges, with \(\sum {n}\left | u {n} \right |\) signifying the absolute value, then the series \(\left | u {n} \right |\) is said to converge absolutely. in addition, if a series is multiplied by another absolutely convergent series, the product series will also converge absolutely. Definition 3.4.1 absolute and conditional convergence. a series \(\sum\limits {n=1}^\infty a n\) is said to converge absolutely if the series \(\sum\limits {n=1}^\infty |a n|\) converges. For each of the following series, determine which convergence test is the best to use and explain why. then determine if the series converges or diverges. if the series is an alternating series, determine whether it converges absolutely, converges conditionally, or diverges. ∞ ∑ n=1 (−1)n 1(3n 1) n! ∑ n = 1 ∞ (− 1) n 1 (3 n 1) n!. Free series absolute convergence calculator check absolute and conditional convergence of infinite series step by step. There are 2 steps to solve this one. absolute convergence. for each series, determine what information, if any, the root or ratio test gives. show the details of your limit computation. a) ∑n=1∞ nπn3n conclusion: b) ∑n=0∞ 1000000nn! conclusion: not the question you’re looking for? post any question and get expert help quickly.
