
Solved Analyze For Absolute And Conditional Convergence Chegg Problem set 20: absolute and conditional convergence 1. use the alternating series test to determine the convergence of the following series: ( 1)" (a) Σ n2n (b) § ( 1) in(n 1) n 2. determine if each of the following series is absolutely or conditionally convergent: ( 1)"tann (a) (b) Σ' ( 1) 1 (c) Σ' ( 1)"el n . n3 n2 n=1 n=1 n=1. Analyze the following alternating series for absolute and conditional convergence. ∑n=2∞2n3 n−2(−1)n 1 your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.

Solved Analyze The Series For Absolute And Conditional Chegg Definition: given a series x∞ n=1 a n, then the absolute series (a.s.) is given by x∞ n=1 |a n|. the absolute series is the same as the original series (o.s.), but with all positive terms. definition: a series x∞ n=1 a n is called absolutely convergent if the absolute series converges. example: x∞ n=1 (−1)n n5 absolutely converges. Example \(\pageindex{3}\): determining absolute and conditional convergence. determine if the following series converge absolutely, conditionally, or diverge. 1.\( \sum\limits {n=1}^\infty ( 1)^n\dfrac{n 3}{n^2 2n 5}\qquad 2. \sum\limits {n=1}^\infty ( 1)^n\dfrac{n^2 2n 5}{2^n}\qquad 3.\sum\limits {n=3}^\infty ( 1)^n\dfrac{3n 3}{5n 10}\). An alternating series is said to be conditionally convergent if it’s convergent as it is but would become divergent if all its terms were made positive. an alternating series is said to be absolutely convergent if it would be convergent even if all its terms were made positive. Determining which of these conclusions we can make for a given series will be the focus of this lesson. let's get to it! in this lesson, you will learn: what it means for a series to convergence absolutely or conditionally. how to test a series for absolute convergence. how to test a series for conditional convergence.
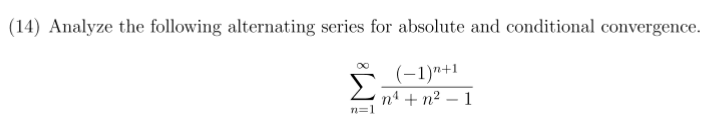
Solved 14 Analyze The Following Alternating Series For Chegg An alternating series is said to be conditionally convergent if it’s convergent as it is but would become divergent if all its terms were made positive. an alternating series is said to be absolutely convergent if it would be convergent even if all its terms were made positive. Determining which of these conclusions we can make for a given series will be the focus of this lesson. let's get to it! in this lesson, you will learn: what it means for a series to convergence absolutely or conditionally. how to test a series for absolute convergence. how to test a series for conditional convergence. Given series. ∑ n = 1 ∞ (− 1) n 1 n 4 n 2 − 1 is of the form ∑ a n, where a n = (− 1) n 1 n 4 n 2 − 1. to check for absolute convergence and conditional convergence. If \(\ds\sum {n=1}^{\infty} a n\) converges, but the corresponding series \(\ds\sum {n=1}^{\infty} |a n|\) does not converge, then \(\ds\sum {n=1}^{\infty} a n\) converges conditionally. note: instead of writing that a series converges absolutely (or conditionally), we may also use the expression the series is absolutely (or conditionally. Keep in mind that, if ak 9 0, then the series p ak diverges; therefore there is no reason to apply any special convergence test. p xk with |x| ≥ 1 (e.g, p(−1)k) diverge since xk 9 0. diverges since k → 1 6= 0. 1 k 1 − diverges since ak = 1 − 1 → e−1 6= 0. The ratio test for absolute convergence . let ∑𝑢. 𝑘. be a series with nonzero terms and suppose lim. 𝑘→∞. 𝑢. 𝑘 1. 𝑢. 𝑘 = 𝜌 a) if 𝜌< 1, the series converges absolutely. b) if 𝜌> 1 or 𝜌= ∞, the series diverges. c) if 𝜌= 1, the series may converge or diverge. j. gonzalez zugasti, university of.

Solved 3 Analyze The Series σ001 An For Absolute And Chegg Given series. ∑ n = 1 ∞ (− 1) n 1 n 4 n 2 − 1 is of the form ∑ a n, where a n = (− 1) n 1 n 4 n 2 − 1. to check for absolute convergence and conditional convergence. If \(\ds\sum {n=1}^{\infty} a n\) converges, but the corresponding series \(\ds\sum {n=1}^{\infty} |a n|\) does not converge, then \(\ds\sum {n=1}^{\infty} a n\) converges conditionally. note: instead of writing that a series converges absolutely (or conditionally), we may also use the expression the series is absolutely (or conditionally. Keep in mind that, if ak 9 0, then the series p ak diverges; therefore there is no reason to apply any special convergence test. p xk with |x| ≥ 1 (e.g, p(−1)k) diverge since xk 9 0. diverges since k → 1 6= 0. 1 k 1 − diverges since ak = 1 − 1 → e−1 6= 0. The ratio test for absolute convergence . let ∑𝑢. 𝑘. be a series with nonzero terms and suppose lim. 𝑘→∞. 𝑢. 𝑘 1. 𝑢. 𝑘 = 𝜌 a) if 𝜌< 1, the series converges absolutely. b) if 𝜌> 1 or 𝜌= ∞, the series diverges. c) if 𝜌= 1, the series may converge or diverge. j. gonzalez zugasti, university of.

Solved 5 Analyze The Following Alternating Series For Chegg Keep in mind that, if ak 9 0, then the series p ak diverges; therefore there is no reason to apply any special convergence test. p xk with |x| ≥ 1 (e.g, p(−1)k) diverge since xk 9 0. diverges since k → 1 6= 0. 1 k 1 − diverges since ak = 1 − 1 → e−1 6= 0. The ratio test for absolute convergence . let ∑𝑢. 𝑘. be a series with nonzero terms and suppose lim. 𝑘→∞. 𝑢. 𝑘 1. 𝑢. 𝑘 = 𝜌 a) if 𝜌< 1, the series converges absolutely. b) if 𝜌> 1 or 𝜌= ∞, the series diverges. c) if 𝜌= 1, the series may converge or diverge. j. gonzalez zugasti, university of.
