
Solved Problem 5 Let G Be A Simple Graph On N Vertices The Chegg Use the corollary “any simple graph with n vertices and more than (n 1)(n 2) 2 edges is connected.” to prove that λ(kn) = n − 1 here’s the best way to solve it. solution. A simple graph is an undirected graph with no loops (edges connecting a vertex to itself) and no multiple edges (more than one edge connecting the same pair of vertices). in this problem, we have a simple graph with n vertices, where n ≥ 2.

The Complete Graph On 1 N Is The Simple Graph Chegg Calculators and convertors for stem, finance, fitness, construction, cooking, and more. Explore math with our beautiful, free online graphing calculator. graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Free graphing calculator instantly graphs your math problems. See how to solve problems and show your work—plus get definitions for mathematical concepts. instantly graph any equation to visualize your function and understand the relationship between variables. search for additional learning materials, such as related worksheets and video tutorials. works in spanish, hindi, german, and more.
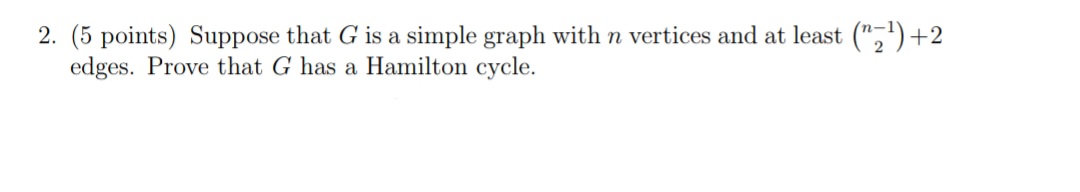
Solved 5 ï Points ï Suppose That G ï Is A Simple Graph With N Chegg Free graphing calculator instantly graphs your math problems. See how to solve problems and show your work—plus get definitions for mathematical concepts. instantly graph any equation to visualize your function and understand the relationship between variables. search for additional learning materials, such as related worksheets and video tutorials. works in spanish, hindi, german, and more. Quickmath will automatically answer the most common problems in algebra, equations and calculus faced by high school and college students. the algebra section allows you to expand, factor or simplify virtually any expression you choose. A simple graph is a set of vertices along with a set of (undi rected) edges with no self loops. most concepts from directed graphs, like walks and paths, can be used almost unchanged for simple graphs. a cycle in a simple graph must be of length at least 3. the degree of a vertex is the number of edges incident to it. Solution: let g be any finite simple graph with more than one vertex and |v g| = n ≥ 2. first, we notice that the maximal degree of any vertex in g is less than equal n−1. also, if our graph g is not connected, then the maximal degree is strictly less than n−1. case 1: assume that g is connected. Draw, scan, solve, and learn! solve long equations, draw in landscape! see how to solve problems and show your work—plus get definitions for mathematical concepts. instantly graph any equation to visualize your function and understand the relationship between variables.
