
Solved 2 Let E E1 E2 E3 Be The Standard Basis For Chegg Here’s the best way to solve it. (b) let e = {e1, e2, e3} be the standard basis for r3, b = {b1, b2, b3} be a basis for a vector space u, and s: r3 → u be a linear transformation with the property that s (x1, x2, x3) = (3x1 x2 2x3)b1 (x1 x3jb2 (3x1 x2 3x3)by, find the matrix f for s relative to e and b. instructions 1. 1. let e = {e1,e2,e3} be the standard basis for r3 and let b = {b1,b2,b3} be a basis for a vector space v. suppose t: r3 → v is a linear transformation with the property that t x1 x2 x3 =(x 3 − x2)b1 −(x1 x3)b2 (x1 − x2)b3. (a) compute t(e1), t(e2)andt(e3). (b) compute the coordinate vectors (relative to b)[t(e1)]b,[t(e2)]b and [t(e3)]b.
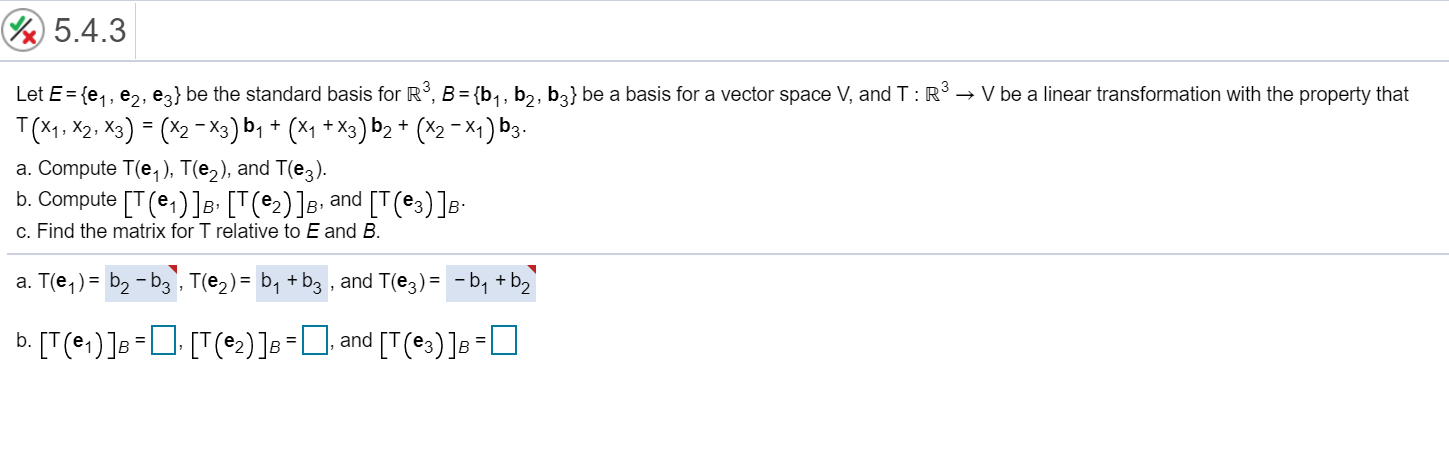
Solved Let E E1 E2 E3 Be The Standard Basis For R 3 B Chegg Columns of a are vectors l(e 1), l(e 2), . . . , l(e n), where e 1, e 2, . . . , e n is the standard basis for r n. calculation: given linear transformation are: t(e 1) = 7e 1 5e 3, t(e 2) = 2e 2 9e 3, t(e 3) = e 1 e 2 e 3. let the standard matrix be a with respect to the basis e 1, e 2, e 3, now t(e 1) = 7e 1 0e 2 5e 3, t(e 2. Let e={e1,e2,e3} be the standard basis for r3,b={b1,b2,b3} be a basis for a vector space v, and t:r3→∨ be a linear transformation with the property that t(x1,x2,x3)=(x3−x2)b1−(x1 x3)b2 (x1−x2)b3. a. compute t(e1),t(e2), and t(e3). b. compute [t(e1)]b,[ t(e2)]b, and [t(e3)]b. c. find the matrix for t relative to e and b. To find t([1,3, 2]'), we can express [1,3, 2]' as a linear combination of the standard basis** vectors**: [1,3, 2]' = 1e1 3e2 2e3. since t is a linear transformation, we can apply it to each component of the linear combination. using the given images of the basis vectors, we have t([1,3, 2]') = 1t(e1) 3t(e2) 2t(e3). Let v = {(a, b) | a, b ∈ r, b > 0} and define addition by (a, b) ⊕ (c, d) = (ad be, bd) and define scalar multiplication by t Θ (a, b) = (tab^t 1 , b^t). use theorem 1 to show that axioms v3 and v4 hold for v with these operations. (note that we are using ⊕ and Θ to represent the operations of.

Solved B Let E E1 E2 E3 Be The Standard Basis For Chegg To find t([1,3, 2]'), we can express [1,3, 2]' as a linear combination of the standard basis** vectors**: [1,3, 2]' = 1e1 3e2 2e3. since t is a linear transformation, we can apply it to each component of the linear combination. using the given images of the basis vectors, we have t([1,3, 2]') = 1t(e1) 3t(e2) 2t(e3). Let v = {(a, b) | a, b ∈ r, b > 0} and define addition by (a, b) ⊕ (c, d) = (ad be, bd) and define scalar multiplication by t Θ (a, b) = (tab^t 1 , b^t). use theorem 1 to show that axioms v3 and v4 hold for v with these operations. (note that we are using ⊕ and Θ to represent the operations of. Let c1 = {e1, e2, e3} and let b = {~ez; e1, e2, e3} be the standard basis of r^3. assume b = {~ez; e1, e2, e3} is another basis of r^3. find the matrix that changes basis from b to c1. Let e = {e 1, e 2, e 3} be the standard basis for r 3, and let f = {b 1, b 2} with b 1 = (1, 2) t and b 2 = (−1, 0) t be a basis for r 2. consider l : r 3 → r 2 , defined by l(x) = (x 1 − x 2 ) b 1 (x 1 − x 3 ) b 2 , ∀x = (x 1 , x 2 , x 3 ) t ∈ r 3 . There are 2 steps to solve this one. let a (e 2) b (− e 1) c (e 3 e 1) = 0 ⇒ e 1 (− b c) e 2 (a) e 3 (c) = 0. let e 1, e 2, e 3 be the standard basis vectors in r3 and consider the ordered basis: [e2, e 1, e3 e1] verify that this is actually a basis and find the coordinates of the vector (1,1, l ) t with respect to that basis. Let {e 1 , e 2 , e 3 } be the standard basis of r 3. if t: r 3 → r 3 is a linear transformation such that: t (e 1 ) = − 4 3 0 , t (e 2 ) = 2 − 3 − 1 , t (e 3 ) = − 3 − 4 − 2 , what is the matrix representation of the vector − 2 3 4 under the transformation t?.
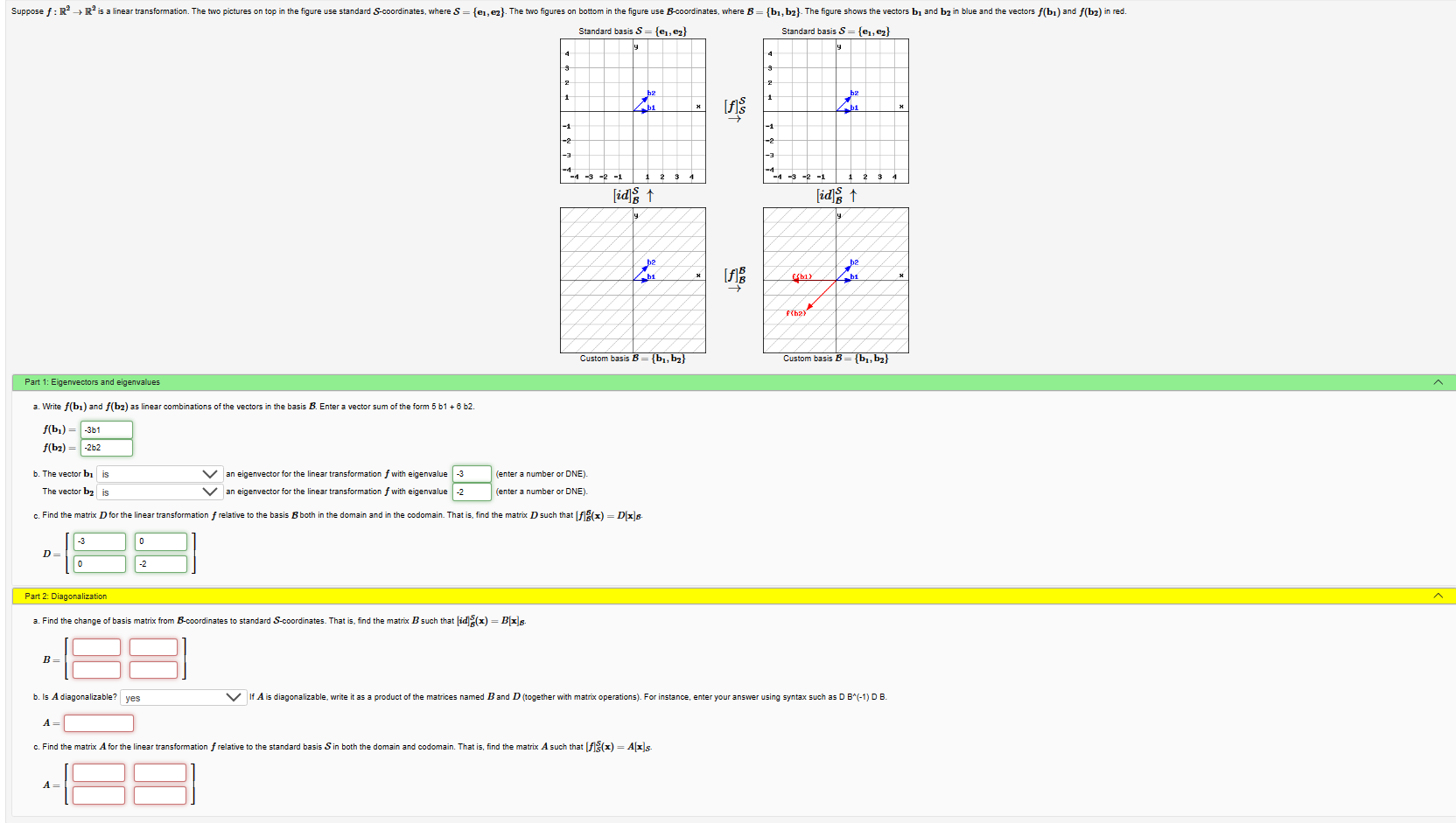
Solved Standard Basis S E1 E2 Standard Basis Chegg Let c1 = {e1, e2, e3} and let b = {~ez; e1, e2, e3} be the standard basis of r^3. assume b = {~ez; e1, e2, e3} is another basis of r^3. find the matrix that changes basis from b to c1. Let e = {e 1, e 2, e 3} be the standard basis for r 3, and let f = {b 1, b 2} with b 1 = (1, 2) t and b 2 = (−1, 0) t be a basis for r 2. consider l : r 3 → r 2 , defined by l(x) = (x 1 − x 2 ) b 1 (x 1 − x 3 ) b 2 , ∀x = (x 1 , x 2 , x 3 ) t ∈ r 3 . There are 2 steps to solve this one. let a (e 2) b (− e 1) c (e 3 e 1) = 0 ⇒ e 1 (− b c) e 2 (a) e 3 (c) = 0. let e 1, e 2, e 3 be the standard basis vectors in r3 and consider the ordered basis: [e2, e 1, e3 e1] verify that this is actually a basis and find the coordinates of the vector (1,1, l ) t with respect to that basis. Let {e 1 , e 2 , e 3 } be the standard basis of r 3. if t: r 3 → r 3 is a linear transformation such that: t (e 1 ) = − 4 3 0 , t (e 2 ) = 2 − 3 − 1 , t (e 3 ) = − 3 − 4 − 2 , what is the matrix representation of the vector − 2 3 4 under the transformation t?.

Solved Let E E 1 E 2 E 3 Be The Standard Basis For Chegg There are 2 steps to solve this one. let a (e 2) b (− e 1) c (e 3 e 1) = 0 ⇒ e 1 (− b c) e 2 (a) e 3 (c) = 0. let e 1, e 2, e 3 be the standard basis vectors in r3 and consider the ordered basis: [e2, e 1, e3 e1] verify that this is actually a basis and find the coordinates of the vector (1,1, l ) t with respect to that basis. Let {e 1 , e 2 , e 3 } be the standard basis of r 3. if t: r 3 → r 3 is a linear transformation such that: t (e 1 ) = − 4 3 0 , t (e 2 ) = 2 − 3 − 1 , t (e 3 ) = − 3 − 4 − 2 , what is the matrix representation of the vector − 2 3 4 under the transformation t?.
