
Solved Bã I 2 Cho Tam Giã C Abc Vuã Ng TẠI A Tia Phã N Giã C Cá A Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. it shows you the solution, graph, detailed steps and explanations for each problem. Enter the equation you want to solve into the editor. the equation calculator allows you to take a simple or complex equation and solve by best method possible. step 2: click the blue arrow to submit and see the result! the equation solver allows you to enter your problem and solve the equation to see the result. solve in one variable or many.

Solved Bã I 1 66 ä Iá U Cho Tam Giã C Abc Nhá N ä æ á Ng Cao Ad Free math problem solver answers your algebra homework questions with step by step explanations. Solution for bà i 1. cho tam giác abc. Ä Æ°á» ng phân giác ad (d thuá»™c bc) kéo tia dx song song vá»›i ab: tia dx cắt ac tại e. chứng minh tam giác ade là tam giác cân. Solution for ba : (Ä‘iểm) cho tam giác abc ná»™i tiếp trong Ä‘Æ°á» ng tròn (o) kẻ các Ä‘Æ°á» ng cao bd và ce của tam giác abc chung cắt nhau tại h. chứng minh tam giác world's only instant tutoring platform search instant tutoring. Cho tam giác đều abc có tâm o. gọi i là một điểm tùy ý bên trong tam giác abc . h id,ie,if tương ứng vuông góc với bc,ca,ab . giả sử vector id vector ie vector if= a b vector io (với a b là phân giản).

Solved Bã I 2 Cho Tam Giã C Nhá N Abc Cã ä æ á Ng Trã N O Cã ä æ Solution for ba : (Ä‘iểm) cho tam giác abc ná»™i tiếp trong Ä‘Æ°á» ng tròn (o) kẻ các Ä‘Æ°á» ng cao bd và ce của tam giác abc chung cắt nhau tại h. chứng minh tam giác world's only instant tutoring platform search instant tutoring. Cho tam giác đều abc có tâm o. gọi i là một điểm tùy ý bên trong tam giác abc . h id,ie,if tương ứng vuông góc với bc,ca,ab . giả sử vector id vector ie vector if= a b vector io (với a b là phân giản). Cho tam giác abc có độ dài ba cạnh là ab=2,bc=5,ca=6 . tính độ dài đườ trung tuyến ma, với m là trung điểm của bc . lời giải. Cho tam giác abc, lấy d ∈ a b, e ∈ a c sao cho b d = c e. gọi k là giao điểm của de và bc. chứng minh rằng tỉ số k e k d = a b a c . Cho tam giác abc. a) chứng minh tồn tại duy nhất một điểm i thỏa mãn \(2\overrightarrow {ia} 3\overrightarrow {ib} 4\overrightarrow {ic} = \overrightarrow 0 \). b) tìm quỹ tích điểm thỏa mãn \(\left| {2\overrightarrow {ma} 3\overrightarrow {mb} 4\overrightarrow {mc} } \right| = \left| {\overrightarrow {mb. Đáp án giải thích các bước giải: ) ) xét tứ giác abdc a b d c có : i d = i a(i d = i a (gt)) bi = i c(b i = i c (gt)) hay hai đường chéo ad a d và bc b c cùng cắt nhau tại trung điểm i i. ⇒ abdc ⇒ a b d c là hình bình hành. ⇒ ab = cd ⇒ a b = c d và ab a b cd c d. hãy giúp mọi người biết câu trả lời này thế nào? Đăng nhập để hỏi chi tiết.
Solved Bã I 3 3 0 ä Iá ƒm Cho Tam Giã C Abc Cã Ab Ac Gá I M Lã Cho tam giác abc có độ dài ba cạnh là ab=2,bc=5,ca=6 . tính độ dài đườ trung tuyến ma, với m là trung điểm của bc . lời giải. Cho tam giác abc, lấy d ∈ a b, e ∈ a c sao cho b d = c e. gọi k là giao điểm của de và bc. chứng minh rằng tỉ số k e k d = a b a c . Cho tam giác abc. a) chứng minh tồn tại duy nhất một điểm i thỏa mãn \(2\overrightarrow {ia} 3\overrightarrow {ib} 4\overrightarrow {ic} = \overrightarrow 0 \). b) tìm quỹ tích điểm thỏa mãn \(\left| {2\overrightarrow {ma} 3\overrightarrow {mb} 4\overrightarrow {mc} } \right| = \left| {\overrightarrow {mb. Đáp án giải thích các bước giải: ) ) xét tứ giác abdc a b d c có : i d = i a(i d = i a (gt)) bi = i c(b i = i c (gt)) hay hai đường chéo ad a d và bc b c cùng cắt nhau tại trung điểm i i. ⇒ abdc ⇒ a b d c là hình bình hành. ⇒ ab = cd ⇒ a b = c d và ab a b cd c d. hãy giúp mọi người biết câu trả lời này thế nào? Đăng nhập để hỏi chi tiết.
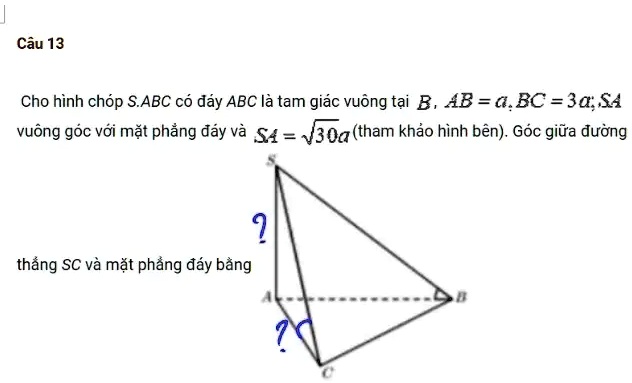
Solved Cã U 13 Cho Hã Nh Chã P Sabc Cã ä ã Y Abc Lã Tam Giã C Vuã Ng Cho tam giác abc. a) chứng minh tồn tại duy nhất một điểm i thỏa mãn \(2\overrightarrow {ia} 3\overrightarrow {ib} 4\overrightarrow {ic} = \overrightarrow 0 \). b) tìm quỹ tích điểm thỏa mãn \(\left| {2\overrightarrow {ma} 3\overrightarrow {mb} 4\overrightarrow {mc} } \right| = \left| {\overrightarrow {mb. Đáp án giải thích các bước giải: ) ) xét tứ giác abdc a b d c có : i d = i a(i d = i a (gt)) bi = i c(b i = i c (gt)) hay hai đường chéo ad a d và bc b c cùng cắt nhau tại trung điểm i i. ⇒ abdc ⇒ a b d c là hình bình hành. ⇒ ab = cd ⇒ a b = c d và ab a b cd c d. hãy giúp mọi người biết câu trả lời này thế nào? Đăng nhập để hỏi chi tiết.
