
Solved Bã I 9 Cho Tam Giã C Abc Vuã Ng TẠI A Tia Phã N Giã C Cá A Solution for bà i 4 (1 Ä‘iểm): cho tam giác abc vuông tại a, có ab = 6 cm, bc = 10 cm, Ä‘Æ°á» ng cao ah. gá» i m và n lần lượt là hình chiếu của Ä‘iểm h trên cạnh bc = 10 cm, Ä‘Æ°á» ng cao ah. gá» i m và n lần lượt là hình chiếu cá. Tia phân giác của góc abc cắt ac tại d. từ d kéo Ä‘Æ°á» ng thẳng vuông góc vá»›i bc cắt bc tại h. trên tia ac lấy Ä‘iểm e sao cho ae = ab. Ä Æ°á» ng thẳng kẻ vuông góc vá»›i ac tại e cắt Ä‘Æ°á» ng thẳng dh tại k. a.

Solved Bã I 2 Cho Tam Giã C Abc Vuã Ng TẠI A Tia Phã N Giã C Cá A Dạng 4. tam giác abc vuông tại a, đường phân giác bd. cho tam giác abc vuông tại a và đường cao ah. tia phân giác góc b cất ah tại i và cắt ac tại d. kẻ dkbot bc k thuộc bc. a chứng minh abd= kbd. b chứng minh ai>ih. c chứng minh ikparallel ac. 088.606.1010 10 chuyên dhat e bồi dưỡng môn. Cho tam giác abc vuông tại a. tia phân giác góc b cắt ac ở d. kẻ dh vuông góc vói bc tại h. so sánh: a) ba và bh; b) da và dc. Cho tam giác abc có ab < ac. trên ac lấy điểm d sao cho ab = ad. tia phân giác của góc a cắt bc tại e. a. chứng minh: tam giác abe = tam giác ade b. cho ae cắt bd tại h. chứng minh: ae vuông góc với bd tại h. c. trên tia đối của tia ed lấy điểm m sao cho em = ec. chứng minh: a, b, m thẳng hàng. Cho tam giác abc cân tại a. trên tia đối của tia ba lấy điểm d trên tia đối của tia ca lấy điểm e sao cho bd = ce, gọi i là giao điểm của be và cd. a) chứng minh ib = ic, id = ie.
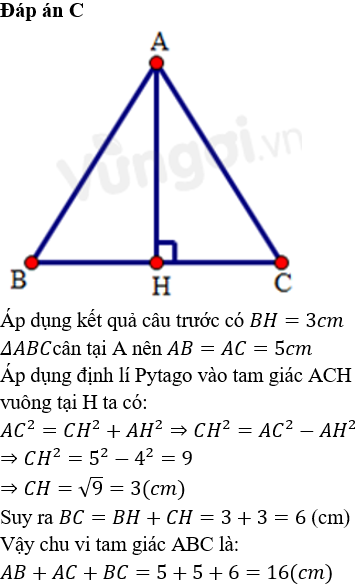
Cho Tam Giã C Abc Cã N TẠI A KẠAh Vuã Ng Gã C Vá I Bc TẠI H Cho Ah 4cm Ab Cho tam giác abc có ab < ac. trên ac lấy điểm d sao cho ab = ad. tia phân giác của góc a cắt bc tại e. a. chứng minh: tam giác abe = tam giác ade b. cho ae cắt bd tại h. chứng minh: ae vuông góc với bd tại h. c. trên tia đối của tia ed lấy điểm m sao cho em = ec. chứng minh: a, b, m thẳng hàng. Cho tam giác abc cân tại a. trên tia đối của tia ba lấy điểm d trên tia đối của tia ca lấy điểm e sao cho bd = ce, gọi i là giao điểm của be và cd. a) chứng minh ib = ic, id = ie. Cho tam giác abc vuông tại a (ac > ab) đường cao ah (h ∈ bc). trên tia hc lấy điểm d sao cho hd = ha. Đường vuông góc với bc tại d cắt ac tại e 1. chứng minh rằng bec~ adc. tính độ dài đoạn be theo m = ab 2. gọi m là trung điểm của đoạn be. chứng minh rằng bhm~ bec. tính số đo góc ahm. 2) so cha câu 4. cho tam giác abc vuông tại a có ab ac. vẽ ad là tia phân giác của bac( d thuộc bc). trên ac lấy điểm e sao cho ae=ab. a) chứng minh abd = aed. b) tia ed cắt ab tại f. chứng minh ac=af. c) gọi g là trung điểm của df, ad cắt cf tại h và cắt cg tại i. chứng minh: di=2ih. B) t×m x Î z ®Ó c lµ sè tù nhiªn. c©u 4: (3 ®iÓm) cho tam gi¸c vu«ng c©n abc (ab = ac), tia ph©n gi¸c cña c¸c gãc b vµ c c¾t ac vµ ab lÇn lît t¹i e vµ d. a) chøng minh r»ng: be = cd; ad = ae. b) gäi i lµ giao ®iÓm cña be vµ cd. ai c¾t bc ë m, chøng minh r»ng c¸c dmab; mac lµ tam gi¸c vu«ng c©n. Bà i 4: cho tam giác abc vuông tại a (ab < ac) có ah là đưỠng cao (hÆ°á»›ng xuống cạnh bc). a) chứng minh: Δabc ≅ Δahc và ac^2 = bc · hc. b) cd là đưỠng phân giác của Δacb (d thuá»™c cạnh ab).

Cho Tam Giгўc Abc Vuгґng Tбєўi A д ж б ќng Cao Ah Cho Ab Ac 3 4 Vг Ah 12cm Cho tam giác abc vuông tại a (ac > ab) đường cao ah (h ∈ bc). trên tia hc lấy điểm d sao cho hd = ha. Đường vuông góc với bc tại d cắt ac tại e 1. chứng minh rằng bec~ adc. tính độ dài đoạn be theo m = ab 2. gọi m là trung điểm của đoạn be. chứng minh rằng bhm~ bec. tính số đo góc ahm. 2) so cha câu 4. cho tam giác abc vuông tại a có ab ac. vẽ ad là tia phân giác của bac( d thuộc bc). trên ac lấy điểm e sao cho ae=ab. a) chứng minh abd = aed. b) tia ed cắt ab tại f. chứng minh ac=af. c) gọi g là trung điểm của df, ad cắt cf tại h và cắt cg tại i. chứng minh: di=2ih. B) t×m x Î z ®Ó c lµ sè tù nhiªn. c©u 4: (3 ®iÓm) cho tam gi¸c vu«ng c©n abc (ab = ac), tia ph©n gi¸c cña c¸c gãc b vµ c c¾t ac vµ ab lÇn lît t¹i e vµ d. a) chøng minh r»ng: be = cd; ad = ae. b) gäi i lµ giao ®iÓm cña be vµ cd. ai c¾t bc ë m, chøng minh r»ng c¸c dmab; mac lµ tam gi¸c vu«ng c©n. Bà i 4: cho tam giác abc vuông tại a (ab < ac) có ah là đưỠng cao (hÆ°á»›ng xuống cạnh bc). a) chứng minh: Δabc ≅ Δahc và ac^2 = bc · hc. b) cd là đưỠng phân giác của Δacb (d thuá»™c cạnh ab).

Cho Tam Giгўc Abc Vuгґng Tбєўi A Cгі Bc 25cm Ab 20cm Kбє д ж б ќng Cao Ah Cб A B) t×m x Î z ®Ó c lµ sè tù nhiªn. c©u 4: (3 ®iÓm) cho tam gi¸c vu«ng c©n abc (ab = ac), tia ph©n gi¸c cña c¸c gãc b vµ c c¾t ac vµ ab lÇn lît t¹i e vµ d. a) chøng minh r»ng: be = cd; ad = ae. b) gäi i lµ giao ®iÓm cña be vµ cd. ai c¾t bc ë m, chøng minh r»ng c¸c dmab; mac lµ tam gi¸c vu«ng c©n. Bà i 4: cho tam giác abc vuông tại a (ab < ac) có ah là đưỠng cao (hÆ°á»›ng xuống cạnh bc). a) chứng minh: Δabc ≅ Δahc và ac^2 = bc · hc. b) cd là đưỠng phân giác của Δacb (d thuá»™c cạnh ab).
