
Calculus Iii Surface Integrals Of Vector Fields Pdf Here’s the best way to solve it. calculus 3: vector field (surface integrals) 1 (2) given the parametric surface, x and vector field f and continuous normal unit vector n. find sif f:nds : x (u,0) = (u cos 0, u sin 0, 0), (u,0) € [0, 1] x [0, 4t] f (x, y, z) = yi – xj (x2 y²)k, nk > 0. not the question you’re looking for?. Question: calculus 3: vector field (surface integrals) given vector field f and curve surface and continuous normal unit vector non surface s. find the flux of f satisfying direction of n and for surface s. (b) f (x, y, z) = yi zj x²k s is the region above the plane xy within the spherical surface x2 y2 z2 = 4 and n.k > 0.

Solved Calculus 3 Vector Field Surface Integrals 1 2 Chegg In order to work with surface integrals of vector fields we will need to be able to write down a formula for the unit normal vector corresponding to the orientation that we’ve chosen to work with. In this video we will apply our prior knowledge of surface integrals to surface integrals of vector fields. feel free to send feedback and or questions in the comments. Here is a set of practice problems to accompany the surface integrals of vector fields section of the surface integrals chapter of the notes for paul dawkins calculus iii course at lamar university. Question: calculus 3: vector field (surface integrals) given enclosed region d bounded by parabola surface = =and plane z = 1 at r? f (x, y, z) = (2x, 2y, 2z 1) when the normal unit vector n of ad direct outward d, find the surface integrals definitions, find the value of shop finds ad note: do not use divergence rule to solve this question.
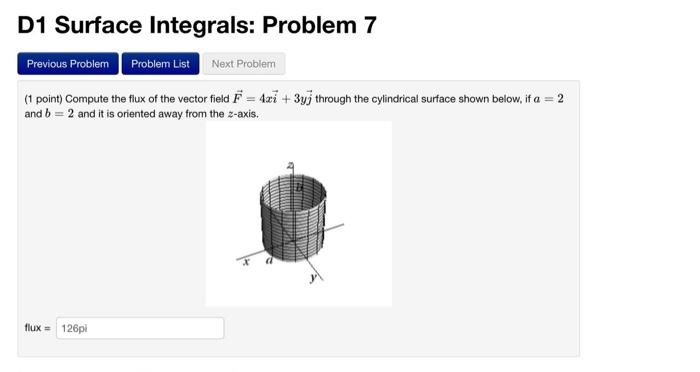
Solved D1 Surface Integrals Problem 7 1 Point Compute The Chegg Here is a set of practice problems to accompany the surface integrals of vector fields section of the surface integrals chapter of the notes for paul dawkins calculus iii course at lamar university. Question: calculus 3: vector field (surface integrals) given enclosed region d bounded by parabola surface = =and plane z = 1 at r? f (x, y, z) = (2x, 2y, 2z 1) when the normal unit vector n of ad direct outward d, find the surface integrals definitions, find the value of shop finds ad note: do not use divergence rule to solve this question. Curl and divergence – in this section we will introduce the concepts of the curl and the divergence of a vector field. we will also give two vector forms of green’s theorem and show how the curl can be used to identify if a three dimensional vector field is conservative field or not. Calculus questions and answers (5) determine the line integral of the vector field f=1x2 y2 (: y,x:) on the orientedcurve c that is made up piecewise first by a line segment from (1,1) to (2,0) followedby the part of the curve y (x 2)3 from (2,0) to (3,1) and ending with the partof the curve y=3x from. Find the flux of the vector field through the surface parameterized by the vector. solution. first we calculate the partial derivatives: it follows that. hence, the vector area element is. as and the vector field can be represented in the following form: then the original surface integral across is. see more problems on page 2. Just as we can integrate functions $f (x,y)$ over regions in the plane, using $$\dint {d} f (x,y)\, da,$$ so we can compute integrals over surfaces in space, using $$\dint {d} f (x,y,z)\, ds.$$ in practice this means that we have a vector function $ {\bf r} (u,v)=\langle x (u,v),y (u,v),z (u,v)\rangle$ for the surface, and the integral we.

Lesson47 48 16 5 Surface Integrals Vector Fields Chegg Curl and divergence – in this section we will introduce the concepts of the curl and the divergence of a vector field. we will also give two vector forms of green’s theorem and show how the curl can be used to identify if a three dimensional vector field is conservative field or not. Calculus questions and answers (5) determine the line integral of the vector field f=1x2 y2 (: y,x:) on the orientedcurve c that is made up piecewise first by a line segment from (1,1) to (2,0) followedby the part of the curve y (x 2)3 from (2,0) to (3,1) and ending with the partof the curve y=3x from. Find the flux of the vector field through the surface parameterized by the vector. solution. first we calculate the partial derivatives: it follows that. hence, the vector area element is. as and the vector field can be represented in the following form: then the original surface integral across is. see more problems on page 2. Just as we can integrate functions $f (x,y)$ over regions in the plane, using $$\dint {d} f (x,y)\, da,$$ so we can compute integrals over surfaces in space, using $$\dint {d} f (x,y,z)\, ds.$$ in practice this means that we have a vector function $ {\bf r} (u,v)=\langle x (u,v),y (u,v),z (u,v)\rangle$ for the surface, and the integral we.
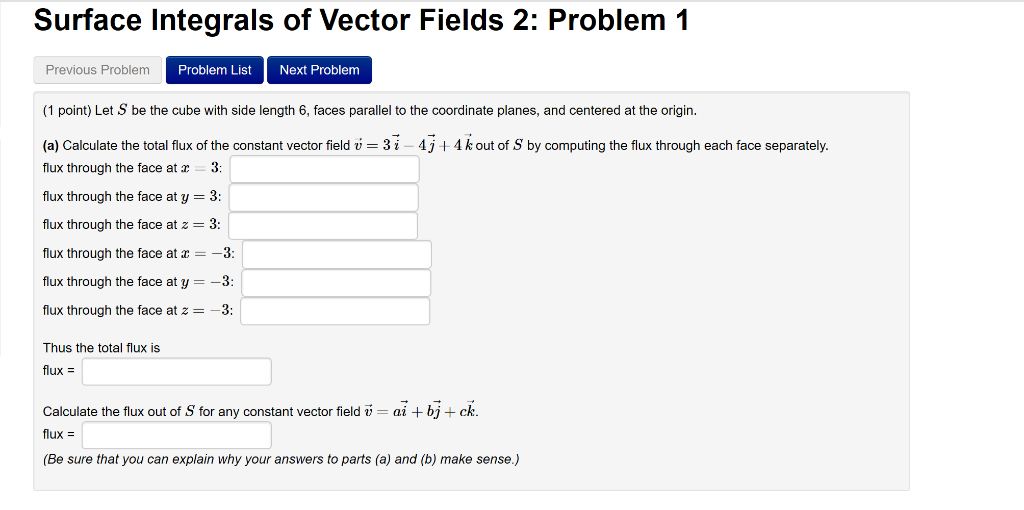
Solved Surface Integrals Of Vector Fields 2 Problem1 Chegg Find the flux of the vector field through the surface parameterized by the vector. solution. first we calculate the partial derivatives: it follows that. hence, the vector area element is. as and the vector field can be represented in the following form: then the original surface integral across is. see more problems on page 2. Just as we can integrate functions $f (x,y)$ over regions in the plane, using $$\dint {d} f (x,y)\, da,$$ so we can compute integrals over surfaces in space, using $$\dint {d} f (x,y,z)\, ds.$$ in practice this means that we have a vector function $ {\bf r} (u,v)=\langle x (u,v),y (u,v),z (u,v)\rangle$ for the surface, and the integral we.
