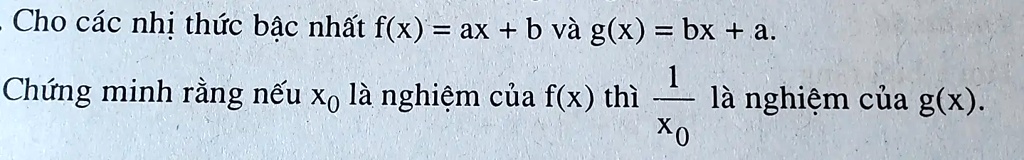
Solved Cho Cã C Nhi Thá C BẠC NhẠT F X Ax B Vã G X Bx A Hàm số g (x) = |x² 4|x| 5| có đồ thị đối xứng qua trục oy. Để phương trình có 2 nghiệm phân biệt, m phải dương và nhỏ hơn giá trị cực tiểu của g (x). giá trị cực tiểu của g (x) là 0. vậy không có giá trị m nào thỏa mãn. tuy nhiên, nếu đề bài là có 4 nghiệm phân biệt thì ta xét g (x) = m. g (x) đạt cực tiểu tại x=0, g (0) = 5. Cho đa thức bậc hai f( x ) = a(x^2) bx c, trong đó a, b và c là những số đã biết (với a khác 0). a) cho biết a b c = 0. giải thích tại sao x = 1 là.

Solution Lua N Va N Tha C Si Kinh Te Ca C Nha N To A Nh Hu O Ng E N Ca Cho đa thức `f(x)=ax^2 bx c` có `2a;a b` và `c` là các số nguyên . chứng minh `f(x)` nhận giá trị nguyên với mọi số nguyên `x` th1: `a` là số nguyên `(1)` mà `2a` là số nguyên do `2` là một số nguyên `=>` `a` là số nguyên th2: `a` có dạng `m 2` với `m` là số. Đáp án đúng là: c. cho tam thức bậc hai f (x) = ax2 bx c (a ≠ 0), ta có: ⦁ nếu ∆ < 0 thì f (x) cùng dấu với a với mọi giá trị x. do đó phương án b, d đều sai. ⦁ nếu ∆ = 0 và x0 = − b 2a x 0 = − b 2 a là nghiệm kép của f (x) thì f (x) cùng dấu với a với mọi x ≠ x0. do đó phương án c đúng. Cho hàm số y=f (x)=ax^3 bx^2 cx d có đồ thị (c) như hình vẽ. biết f' (1)=0 , tính f (5). Để giải bài toán này, ta thực hiện các bước sau: quan sát đồ thị, ta thấy đồ thị cắt trục hoành tại $$x = 1$$x = −1 và $$x = 2$$x = 2. do đó, $$f ( 1) = 0$$f (−1) = 0 và $$f (2) = 0$$f (2) = 0. $$ a b c = 0$$−a b−c = 0. $$b = a c$$b= a c. Chương 1 hàm số möc löc möc löc sè mët sè ành dö mët sè ành nhúng cho sè lôy thøa xα mô ax logarit loga 10 11 13 hyperbolic 15 th nh möc löc möc löc möc löc ch÷ìng 1. nh x h m sÈ nh x¤ 1.1. mët sè ành ngh¾a 1.1. c¡c lo¤i ¡nh x¤.

Solved 10 Cho Hã M Sá Xã C ä á Nh Vã Liãªn Tá C Trãªn Cã BẠNg Cho hàm số y=f (x)=ax^3 bx^2 cx d có đồ thị (c) như hình vẽ. biết f' (1)=0 , tính f (5). Để giải bài toán này, ta thực hiện các bước sau: quan sát đồ thị, ta thấy đồ thị cắt trục hoành tại $$x = 1$$x = −1 và $$x = 2$$x = 2. do đó, $$f ( 1) = 0$$f (−1) = 0 và $$f (2) = 0$$f (2) = 0. $$ a b c = 0$$−a b−c = 0. $$b = a c$$b= a c. Chương 1 hàm số möc löc möc löc sè mët sè ành dö mët sè ành nhúng cho sè lôy thøa xα mô ax logarit loga 10 11 13 hyperbolic 15 th nh möc löc möc löc möc löc ch÷ìng 1. nh x h m sÈ nh x¤ 1.1. mët sè ành ngh¾a 1.1. c¡c lo¤i ¡nh x¤. Xét tam thức bậc hai f(x) = ax 2 bx c, trong đó a < b và f(x) ≥ 0 với mọi x ∈ r. hãy tìm giá trị nhỏ nhất của biểu thức m =. Cho hàm số f (x) thỏa mãn f' (x) = ax² \frac {b} {x³}, f' (1) = 3, f (1) = 2, f (\frac {1} {2}) = \frac {1} {12}. khi đó 2a b bằng bao nhiêu? the core concept is to find the original function f (x) by integrating its derivative f' (x), and then use the given conditions to solve for the constants a and b. 2a b=2(2) 1=5. 2a b=5. Cho tam thức bậc hai f(x) = ax2 bx c (a ≠ 0). trong các phát biểu sau, phát biểu nào đúng? a. f(x) < 0 với mọi x khi và chỉ khi a < 0 và ∆ ≤ 0. Cho hàm số y=f(x)=ax^2 bx c có đồ thị (c) (như hình vẽ). có bao nhiêu giá trị nguyên của tham số m đề phương trình f^2(|x|) (m 2)f(|x|) m 3=0 có 6 nghiệm phân biệt? a. 1 b. 3.

Solved Bã I Tip 2 Cho Hã Nh Chã P S Abcd Cã ä ã Y Abcd Lã Hã Nh Bã Xét tam thức bậc hai f(x) = ax 2 bx c, trong đó a < b và f(x) ≥ 0 với mọi x ∈ r. hãy tìm giá trị nhỏ nhất của biểu thức m =. Cho hàm số f (x) thỏa mãn f' (x) = ax² \frac {b} {x³}, f' (1) = 3, f (1) = 2, f (\frac {1} {2}) = \frac {1} {12}. khi đó 2a b bằng bao nhiêu? the core concept is to find the original function f (x) by integrating its derivative f' (x), and then use the given conditions to solve for the constants a and b. 2a b=2(2) 1=5. 2a b=5. Cho tam thức bậc hai f(x) = ax2 bx c (a ≠ 0). trong các phát biểu sau, phát biểu nào đúng? a. f(x) < 0 với mọi x khi và chỉ khi a < 0 và ∆ ≤ 0. Cho hàm số y=f(x)=ax^2 bx c có đồ thị (c) (như hình vẽ). có bao nhiêu giá trị nguyên của tham số m đề phương trình f^2(|x|) (m 2)f(|x|) m 3=0 có 6 nghiệm phân biệt? a. 1 b. 3.

Solved Tìm Công Th C A Tôi Tôi Ti U C A Các Hàm Sau A Z X Y Y T Cho tam thức bậc hai f(x) = ax2 bx c (a ≠ 0). trong các phát biểu sau, phát biểu nào đúng? a. f(x) < 0 với mọi x khi và chỉ khi a < 0 và ∆ ≤ 0. Cho hàm số y=f(x)=ax^2 bx c có đồ thị (c) (như hình vẽ). có bao nhiêu giá trị nguyên của tham số m đề phương trình f^2(|x|) (m 2)f(|x|) m 3=0 có 6 nghiệm phân biệt? a. 1 b. 3.

Solved Trong Cã C KhẠNg ä á Nh Sau Cã Bao Nhiãªu KhẠNg ä á Nh ä
