
Solved Consider The Equation 4x2 2xy 4y2 15 0 Which Has A Chegg Question: consider the equation 4x2 2xy 4y2−15=0 which has a graph that is a conic section. do all the following: a. use a rotation of axes to rewrite the equation of the conic in the x ' y ' plane and eliminate the bxy term. b. write the conic in standard form and identify the conic. c. identify the key characteristics of the graph. d. Consider a set of n linearly independent vectors s = {x 1, x 2, dots, x n}. prove that if a.
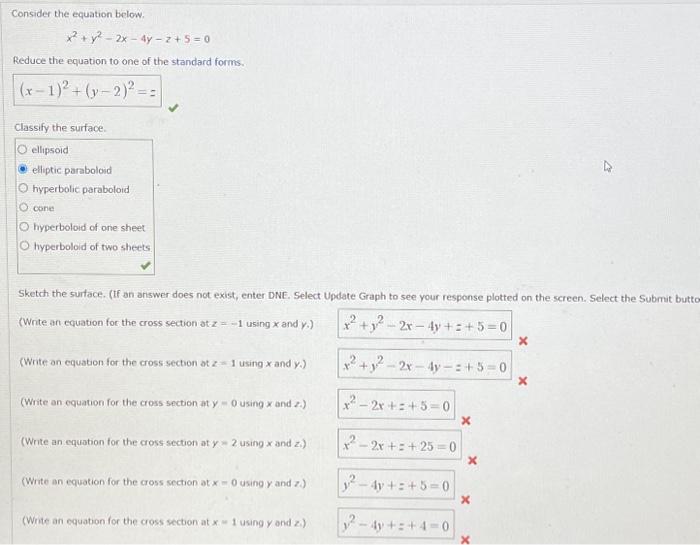
Solved Consider The Equation Below X2 Y2 2x 4y Z 5 0 Reduce Chegg Step 1: enter the equation you want to solve into the editor. the equation calculator allows you to take a simple or complex equation and solve by best method possible. step 2: click the blue arrow to submit and see the result!. There are 2 steps to solve this one. assume x = e z and take logarithm on both sides to transform x into z. consider the following initial value problem. 4x2y" y = 0, y ( 1) = 4, y' ( 1) = 2 use the substitution t = x and find general solution of the resulting differential equation. y (t) = solve the given initial value problem. y (x) = x < 0. Here’s the best way to solve it. 1. solve the following homogeneous equations. a) x²y' = 4x2 7xy 2y2 b) (x² 2xy – 4y2)dx (x2 8xy – 4y?)dy sers 2. test each of the following for exactness and solve the equation. the equations that are not exact may, of course, be solved by methods discussed in the previous discussion. Our expert help has broken down your problem into an easy to learn solution you can count on. there are 2 steps to solve this one.

Solved Consider The Equation Below 4x 2 Y 2 4z 2 4y Chegg Here’s the best way to solve it. 1. solve the following homogeneous equations. a) x²y' = 4x2 7xy 2y2 b) (x² 2xy – 4y2)dx (x2 8xy – 4y?)dy sers 2. test each of the following for exactness and solve the equation. the equations that are not exact may, of course, be solved by methods discussed in the previous discussion. Our expert help has broken down your problem into an easy to learn solution you can count on. there are 2 steps to solve this one. Consider the following differential equation. (x2 4) dy dx 4y = (x 2)2 find the coefficient function p (x) when the given differential equation is written in the standard form dy dx p (x)y = f (x). There are 4 steps to solve this one. differentiate both sides of the equation. differentiate the left side of the equation. not the question you’re looking for? post any question and get expert help quickly. Question: consider the equation 4x2 2xy 4y2−15=0 which has a graph that is a conic section. do all the following: a. use a rotation of axes to rewrite the equation of the conic in the x ' y ' plane and eliminate the bxy term. b. write the conic in standard form and identify the conic. c. identify the key characteristics of the graph. d. Consider the differential equation 4 y'' − 4 y' y = 0; ex 2, xex 2. verify that the functions ex 2 and xex 2 form a fundamental set of solutions of the differential equation on the interval (−∞, ∞). the functions satisfy the differential equation and are linearly independent since w (ex 2, xex 2) = ≠ 0 for −∞ < x < ∞.

Solved Consider The Equation Below 4y2 Z2 X 24y Chegg Consider the following differential equation. (x2 4) dy dx 4y = (x 2)2 find the coefficient function p (x) when the given differential equation is written in the standard form dy dx p (x)y = f (x). There are 4 steps to solve this one. differentiate both sides of the equation. differentiate the left side of the equation. not the question you’re looking for? post any question and get expert help quickly. Question: consider the equation 4x2 2xy 4y2−15=0 which has a graph that is a conic section. do all the following: a. use a rotation of axes to rewrite the equation of the conic in the x ' y ' plane and eliminate the bxy term. b. write the conic in standard form and identify the conic. c. identify the key characteristics of the graph. d. Consider the differential equation 4 y'' − 4 y' y = 0; ex 2, xex 2. verify that the functions ex 2 and xex 2 form a fundamental set of solutions of the differential equation on the interval (−∞, ∞). the functions satisfy the differential equation and are linearly independent since w (ex 2, xex 2) = ≠ 0 for −∞ < x < ∞.
