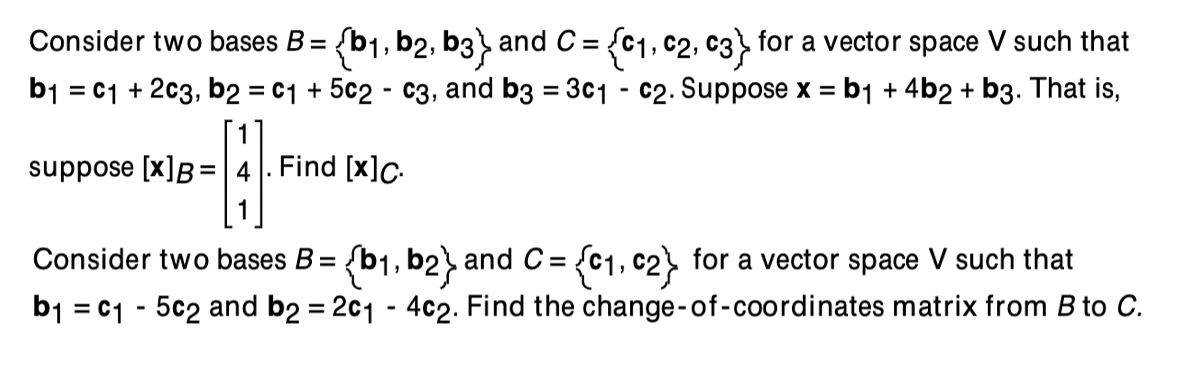
Solved Consider Two Bases B B1 B2 B3 And C C1 C2 C3 Chegg Consider two bases b={b1,b2} and c={c1,c2} for a vector space v such that b1=c1 5c2 and b2=3c1 2c2. suppose x=b1 4b2. find [x ] c. Consider two bases \mathcal{b} = \{b {1},b {2}\} and \mathcal{c} = \{c {1},c {2}\} for a vector space v, such that. b {1} = 4c {1} c {2} \text{and} b {2} = 6c {1} c {2} (1) suppose.

Solved 10 Consider Two Bases B B1 B2 B3 And C C1 C2 Chegg Q let [x] b denote the coordinate vector of x with respect to a basis b. for bases b and c, p c b denotes the change of co. [solved] consider two bases b=b1, b2 and c=c1, c2 for a vector space v such that b1=c1 2c2 and b2=6c1 5c2. suppose x=b1 3b2. that is, suppos. Video answer: b is equal to b1, b2 is equal to b1, c2 is equal to c1, and b2 is equal to c2 in matrix form. 2c1 4c2 is equal to b2 if we take 1 5c1 outside and 2 4 if we take 2 4 inside. if we find the inverse of the coefficients matrix, we can. Consider two bases b = (b1,b2) and c= (c1,c2) for a vector space v such that b1=c1 2c2 and b2=5c1 4c2. suppose x=b1 3b2 that is [x]b =[1,3]. find the transition matrix.
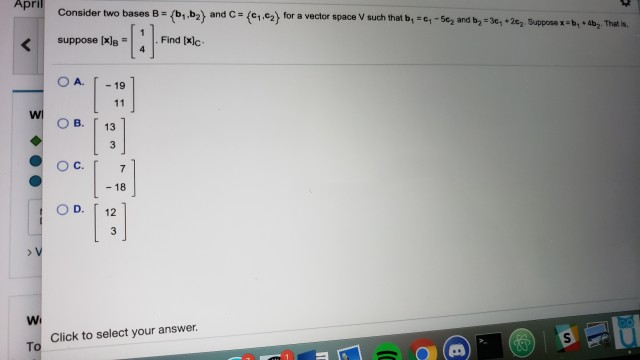
Solved Consider Two Bases B B1 B2 And C C1 C2 For A Chegg Video answer: b is equal to b1, b2 is equal to b1, c2 is equal to c1, and b2 is equal to c2 in matrix form. 2c1 4c2 is equal to b2 if we take 1 5c1 outside and 2 4 if we take 2 4 inside. if we find the inverse of the coefficients matrix, we can. Consider two bases b = (b1,b2) and c= (c1,c2) for a vector space v such that b1=c1 2c2 and b2=5c1 4c2. suppose x=b1 3b2 that is [x]b =[1,3]. find the transition matrix. There are 2 bases, $b$ and $c$ that are bases for $\bbb r^2$. let $b=\{b 1, b 2\}$ and $c=\{c 1,c 2\}$. find the change of coordinates matrix from $b$ to $c$. $b 1= \left[ \begin{matrix} 7 \\ 5 \end. The basis vectors for b and c are related as given: b1 = c1 3c2 and b2 = 2c1 4c2. we also know that vector x in terms of basis b is x = b1 5b2. so, we can express vector x in terms of basis c by replacing b1 and b2 with their expressions in terms of c1 and c2: x = (c1 3c2) 5*(2c1 4c2) = 11c1 17c2 thus, the coordinates of vector x. Essentially, if we have two coordinate vectors, [x]b = [3; 1] and [x]c = [6,4], we want to be able to figure out how b1 and b2 are formed from c1 and c2. example consider two bases b = {b1, b2} and c = {c1, c2}, such that: b1 = 4c1 c2 and b2 = 6c1 c2 suppose x = 3b1 b2 that is, suppose [x]b = [3;1]. Video answer: these are the two vectors u. one and u. two. the first thing we want to do is check the basis for r two. we need to check that they're not in a straight line. we need to make sure the dot product is equal to zero. the 41 dot is minus 3.

Solved Consider Two Bases B B1 Bz And C C1 Cz Of A Chegg There are 2 bases, $b$ and $c$ that are bases for $\bbb r^2$. let $b=\{b 1, b 2\}$ and $c=\{c 1,c 2\}$. find the change of coordinates matrix from $b$ to $c$. $b 1= \left[ \begin{matrix} 7 \\ 5 \end. The basis vectors for b and c are related as given: b1 = c1 3c2 and b2 = 2c1 4c2. we also know that vector x in terms of basis b is x = b1 5b2. so, we can express vector x in terms of basis c by replacing b1 and b2 with their expressions in terms of c1 and c2: x = (c1 3c2) 5*(2c1 4c2) = 11c1 17c2 thus, the coordinates of vector x. Essentially, if we have two coordinate vectors, [x]b = [3; 1] and [x]c = [6,4], we want to be able to figure out how b1 and b2 are formed from c1 and c2. example consider two bases b = {b1, b2} and c = {c1, c2}, such that: b1 = 4c1 c2 and b2 = 6c1 c2 suppose x = 3b1 b2 that is, suppose [x]b = [3;1]. Video answer: these are the two vectors u. one and u. two. the first thing we want to do is check the basis for r two. we need to check that they're not in a straight line. we need to make sure the dot product is equal to zero. the 41 dot is minus 3.
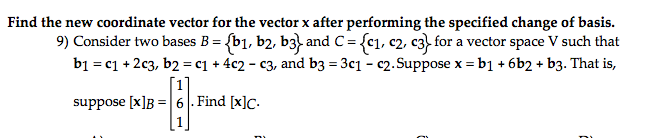
Solved Consider Two Bases B B1 B2 And C C1 C2 Chegg Essentially, if we have two coordinate vectors, [x]b = [3; 1] and [x]c = [6,4], we want to be able to figure out how b1 and b2 are formed from c1 and c2. example consider two bases b = {b1, b2} and c = {c1, c2}, such that: b1 = 4c1 c2 and b2 = 6c1 c2 suppose x = 3b1 b2 that is, suppose [x]b = [3;1]. Video answer: these are the two vectors u. one and u. two. the first thing we want to do is check the basis for r two. we need to check that they're not in a straight line. we need to make sure the dot product is equal to zero. the 41 dot is minus 3.
