
Solved 1 Consider The Two Bases B 2 3 1 1 2 0 2 0 3 Chegg Consider two bases b = {b 1, b 2, b 3} and c = {c 1, c 2, c 3} for a vector space v such that b 1 = c 1 6 c 3, b 2 = c 1 3 c 2 c 3. and b 3 = 5 c 1 c 2. suppose x = b 1 4 b 2 b 3. that is, suppose [x] b = [1 4 1]. find [x] c. here’s the best way to solve it. There are 2 steps to solve this one. consider two bases b ={b1,b2,b3} and c = {c1,c2,c3} for a vector space v such that b1 = c1 6c3,b2 = c1 3c2 −c3. and b3 =5c1−c2. suppose x=b1 4b2 b3. that is, suppose [x]b =⎣⎡ 1 4 1 ⎦⎤. find [x]c ⎣⎡ 10 11 10 ⎦⎤ ⎣⎡ 10 11 2 ⎦⎤ ⎣⎡ 10 11 2 ⎦⎤ ⎣⎡ 10 17 −4 ⎦⎤ ⎣⎡ 7 12 1 ⎦⎤. not the question you’re looking for?.

Solved Consider Two Bases B B1 B2 B3 And C C1 C2 C3 For Chegg Question: 10) consider two bases b : b1,b2, b3 and c = {c1,c2, c3) for a vector space v such that b1 = c1 2c3, b2 = c1 5c2 c3, and b3 =. Let b1 = [1 3], b2 = [ 2 4], c1 = [ 7 9], c2 = [ 5 7] and consider the bases for r^2 given by b = {b1, b2} and c = {c1, c2}. a. find the change of coordinates matrix from c to b. b. find the change of coordinates matrix from b to c. To find the coordinates of the vector x in basis c, we need to express x in terms of the basis vectors c1, c2, and c3. given that x = b1 6b2 b3 and the relationships between the basis vectors b and c are known: b1 = c1 3c3; b2 = c1 4c2 c3; b3 = 5c1 c2; we can substitute the expressions for b1, b2, and b3 into the equation for x and. 10) consider two bases b = b1, b2 and c = c1, c2 for a vector space v such that b1 = c1 3c2 and b2 = 2c1 4c2. suppose x = b1 5b2. that is, suppose [x]b = 1 5 .

Solved Consider Two Bases B B1 B2 B3 And C C1 C2 C3 For Chegg To find the coordinates of the vector x in basis c, we need to express x in terms of the basis vectors c1, c2, and c3. given that x = b1 6b2 b3 and the relationships between the basis vectors b and c are known: b1 = c1 3c3; b2 = c1 4c2 c3; b3 = 5c1 c2; we can substitute the expressions for b1, b2, and b3 into the equation for x and. 10) consider two bases b = b1, b2 and c = c1, c2 for a vector space v such that b1 = c1 3c2 and b2 = 2c1 4c2. suppose x = b1 5b2. that is, suppose [x]b = 1 5 . Let b = {b1, b2} and c = {c1, c2, c3} be bases for vector spaces v and w, respectively. t (b2) = 3c1 3c2 c3 find the matrix for t relative to b and c (you nee the solution is given below. if you have any doubts, please comment. 3 c2 3 c3 5 1 3 3x 2 there fore , [ t ] = 5 i ww b 5 is this answer helpful?. (a) change of coordinates matrix from c to b: to find the change of coordinates matrix from c to b, we need to express each vector in the basis c as a linear combination of the vectors in basis b. given: ~c1 = 2~b1 ~b2 ~b3 ~c2 = 3~b2 ~b3 ~c3 = 3~b1 2~b3 to express ~c1 in terms of b, we write: [~c1]b = [2, 1, 1] similarly, for ~c2 and. $x$ can be considered to be $b 1$ while $p b$ can be seen as $p c$ which would simply be $c$ as it's the change of coordinates matrix from c to the standard basis in $\bbb r^n$. and of course $ [x] b $ can be considered as $[b 1] c$. Essentially, if we have two coordinate vectors, [x]b = [3; 1] and [x]c = [6,4], we want to be able to figure out how b1 and b2 are formed from c1 and c2. example consider two bases b = {b1, b2} and c = {c1, c2}, such that: b1 = 4c1 c2 and b2 = 6c1 c2 suppose x = 3b1 b2 that is, suppose [x]b = [3;1].

Solved Consider Two Bases B B1 B2 B3 And C C1 C2 C3 For Chegg Let b = {b1, b2} and c = {c1, c2, c3} be bases for vector spaces v and w, respectively. t (b2) = 3c1 3c2 c3 find the matrix for t relative to b and c (you nee the solution is given below. if you have any doubts, please comment. 3 c2 3 c3 5 1 3 3x 2 there fore , [ t ] = 5 i ww b 5 is this answer helpful?. (a) change of coordinates matrix from c to b: to find the change of coordinates matrix from c to b, we need to express each vector in the basis c as a linear combination of the vectors in basis b. given: ~c1 = 2~b1 ~b2 ~b3 ~c2 = 3~b2 ~b3 ~c3 = 3~b1 2~b3 to express ~c1 in terms of b, we write: [~c1]b = [2, 1, 1] similarly, for ~c2 and. $x$ can be considered to be $b 1$ while $p b$ can be seen as $p c$ which would simply be $c$ as it's the change of coordinates matrix from c to the standard basis in $\bbb r^n$. and of course $ [x] b $ can be considered as $[b 1] c$. Essentially, if we have two coordinate vectors, [x]b = [3; 1] and [x]c = [6,4], we want to be able to figure out how b1 and b2 are formed from c1 and c2. example consider two bases b = {b1, b2} and c = {c1, c2}, such that: b1 = 4c1 c2 and b2 = 6c1 c2 suppose x = 3b1 b2 that is, suppose [x]b = [3;1].
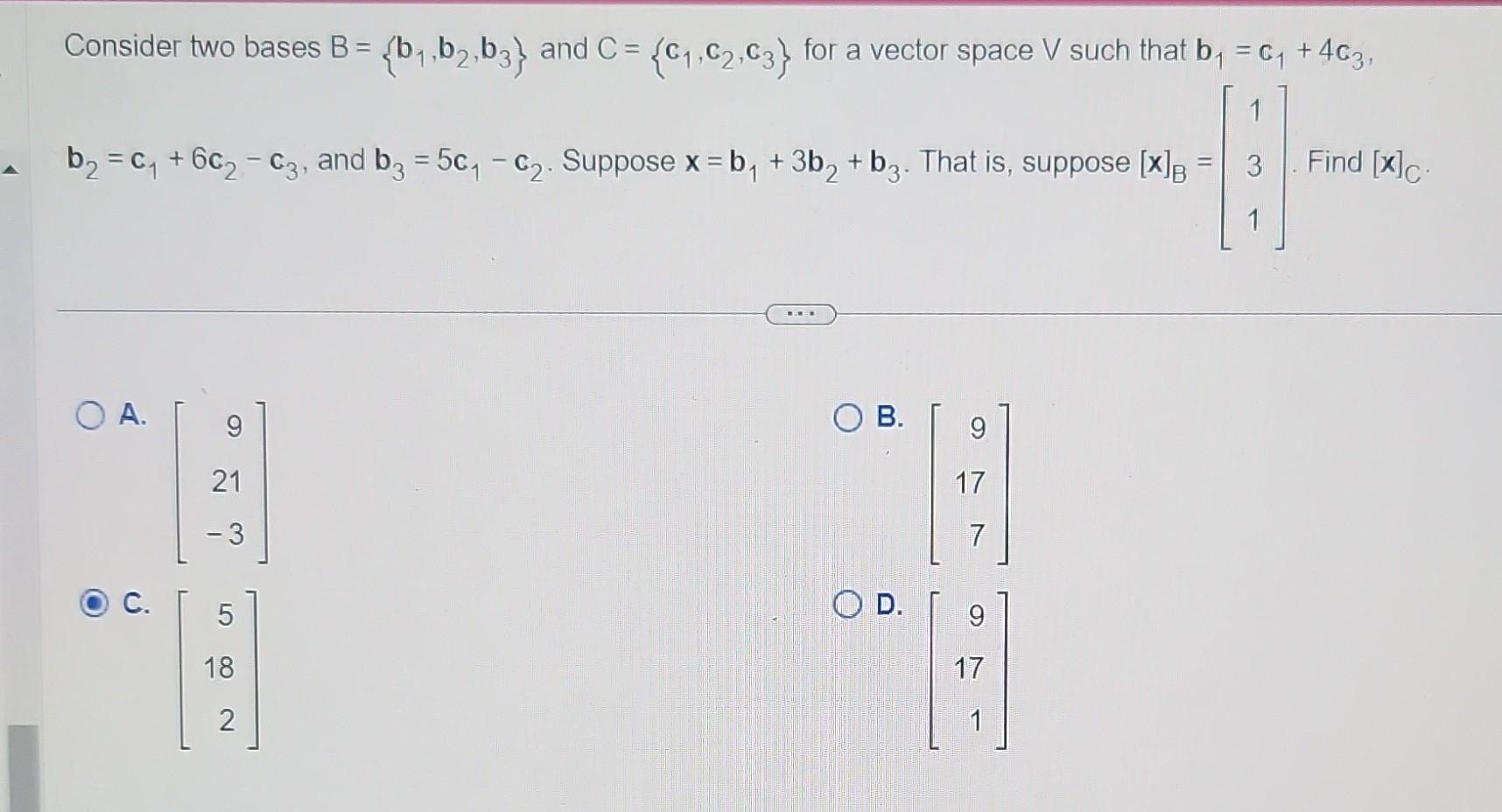
Solved Consider Two Bases B B1 B2 B3 And C C1 C2 C3 For Chegg $x$ can be considered to be $b 1$ while $p b$ can be seen as $p c$ which would simply be $c$ as it's the change of coordinates matrix from c to the standard basis in $\bbb r^n$. and of course $ [x] b $ can be considered as $[b 1] c$. Essentially, if we have two coordinate vectors, [x]b = [3; 1] and [x]c = [6,4], we want to be able to figure out how b1 and b2 are formed from c1 and c2. example consider two bases b = {b1, b2} and c = {c1, c2}, such that: b1 = 4c1 c2 and b2 = 6c1 c2 suppose x = 3b1 b2 that is, suppose [x]b = [3;1].
