Solved Determine If The Following System Of Equations Has No Determine whether the following system of equations have no solution, infinitely many solution or unique solutions. x 2y = 3, 2x 4y = 15 solution: given equations are x 2y = 3. There are three possible results that we can find when working with systems of linear equations: 1. one solution. 2. no solution. 3. infinite solutions. for systems of two equations in two variables, an ordered pair (x,~y) (x, y) is a solution to the system only if it satisfies both equations.
Thanks 130 To determine if the system of equations has no solutions, infinitely many solutions, or exactly one solution, we can use the method of substitution or elimination. let's proceed step by step: we have the system: step 1: solve one equation for one variable. from the first equation, −x y = 7, we solve for y: y = x 7. To determine if the system has no solutions, infinitely many solutions, or exactly one solution, we can use the method of substitution or elimination. however, in this case, it's clear that the second equation is just the first equation multiplied by 1. Learn how to determine if a system of linear equations has no solution or infinitely many solutions. understand the conditions and methods to find the solutions, including solved examples. There are a few ways to tell when a linear system in two variables has no solution: solve the system – if you solve the system and get a nonsense equation (such as 0 = 1), then there is no solution. look at the graph – if the two lines are parallel (they never touch), then there is no solution to the system.
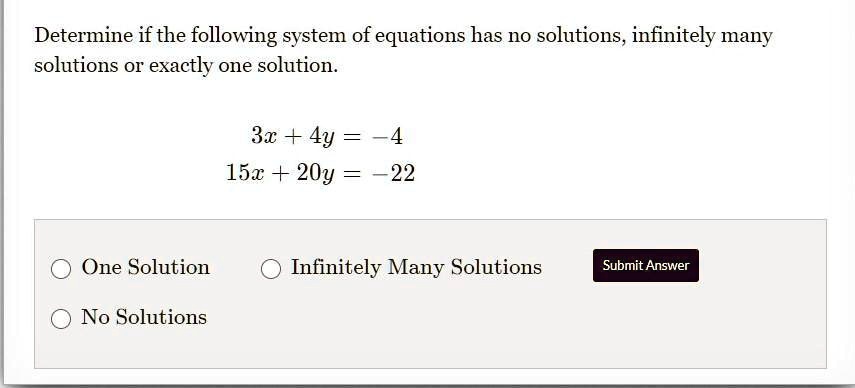
Determine If The Following System Of Equations Has No Solutions Learn how to determine if a system of linear equations has no solution or infinitely many solutions. understand the conditions and methods to find the solutions, including solved examples. There are a few ways to tell when a linear system in two variables has no solution: solve the system – if you solve the system and get a nonsense equation (such as 0 = 1), then there is no solution. look at the graph – if the two lines are parallel (they never touch), then there is no solution to the system. Reconize when a matrix has a unique solutions, no solutions, or infinitely many solutions using python. the example shown previously in this module had a unique solution. the structure of the row reduced matrix was. and the solution was. To determine if the given system of equations has no solutions, infinitely many solutions, or exactly one solution, let's examine the system: we can use the method of elimination or substitution to solve this system. step 1: align the equations. step 2: eliminate one variable. In this section, we will determine the systems that have no solution, and solve the systems that have infinitely many solutions. solve the following system of equations: x y x y = 7 = 9 x y = 7 x y = 9. solution. let us use the gauss jordan method to solve this system. the augmented matrix is. To determine if the given system of equations has no solutions, infinitely many solutions, or exactly one solution, multiply the first equation by 10 and the second equation by 5 in order to compare them more easily.
Solved Determine If The Following System Of Equations Has No Solutions Reconize when a matrix has a unique solutions, no solutions, or infinitely many solutions using python. the example shown previously in this module had a unique solution. the structure of the row reduced matrix was. and the solution was. To determine if the given system of equations has no solutions, infinitely many solutions, or exactly one solution, let's examine the system: we can use the method of elimination or substitution to solve this system. step 1: align the equations. step 2: eliminate one variable. In this section, we will determine the systems that have no solution, and solve the systems that have infinitely many solutions. solve the following system of equations: x y x y = 7 = 9 x y = 7 x y = 9. solution. let us use the gauss jordan method to solve this system. the augmented matrix is. To determine if the given system of equations has no solutions, infinitely many solutions, or exactly one solution, multiply the first equation by 10 and the second equation by 5 in order to compare them more easily.
Solved Determine If The Following System Of Equations Has No Solutions In this section, we will determine the systems that have no solution, and solve the systems that have infinitely many solutions. solve the following system of equations: x y x y = 7 = 9 x y = 7 x y = 9. solution. let us use the gauss jordan method to solve this system. the augmented matrix is. To determine if the given system of equations has no solutions, infinitely many solutions, or exactly one solution, multiply the first equation by 10 and the second equation by 5 in order to compare them more easily.
