Solved Determine Whether The Series Is Absolutely Chegg
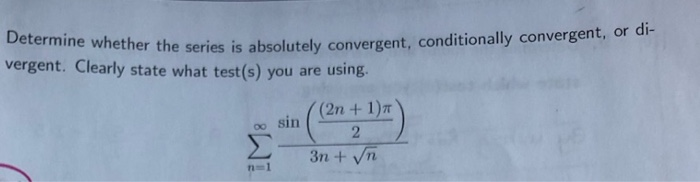
Solved Determine Whether The Series Is Absolutely A Her The Chegg There are 3 steps to solve this one. determine whether the series is absolutely convergent, conditionally convergent, or divergent (input "ac", "cc" or "d" for absolutely convergent, conditionally convergent or divergent, respectively). Here is a set of practice problems to accompany the absolute convergence section of the series & sequences chapter of the notes for paul dawkins calculus ii course at lamar university.
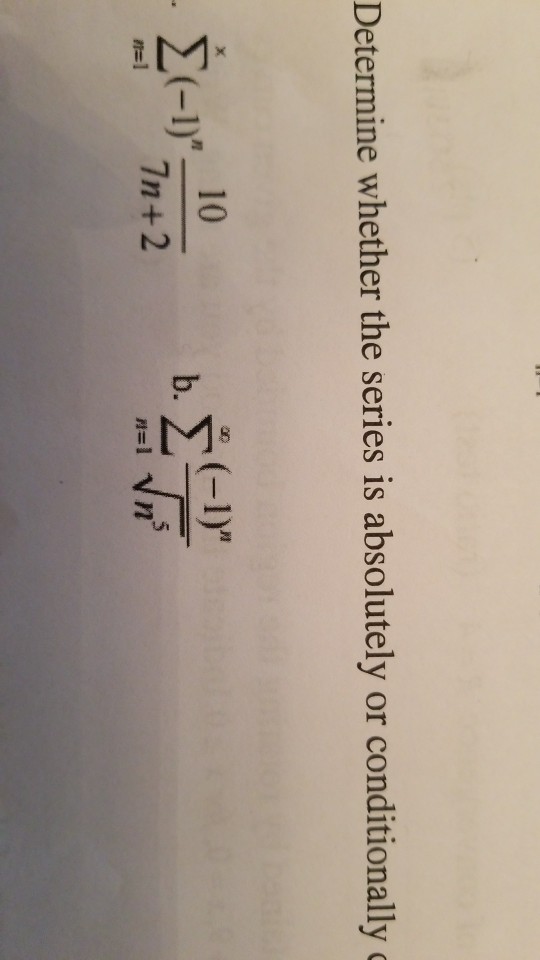
Solved Determine Whether The Series Is Absolutely Or Chegg Learn how to determine if a series is absolutely convergent, conditionally convergent, or divergent, and see examples that walk through sample problems step by step for you to improve your. Click here 👆 to get an answer to your question ️ determine whether the series converges conditionally, converges absolutely, or diverges. use the alternating. The root test is a method used to determine the convergence of an infinite series by examining the nth root of the absolute value of its nth term. specifically, one computes the limit superior of the nth root as n tends to infinity. if this limit is less than one, the series converges absolutely; if it is greater than one, the series diverges; and if it equals one, the test is inconclusive. Chegg get 24 7 homework help | rent textbooks 2.^ chegg survey fielded between sept. 9 among a random sample of u.s. customers who used chegg study or chegg study pack in q2 2024 and q3 2024. solved assignment 2 due date: march 10, 2022 by 11:59 pm 10 mar 2022 assignment 2 due date: march 10, 2022 by 11:59 pm cst .
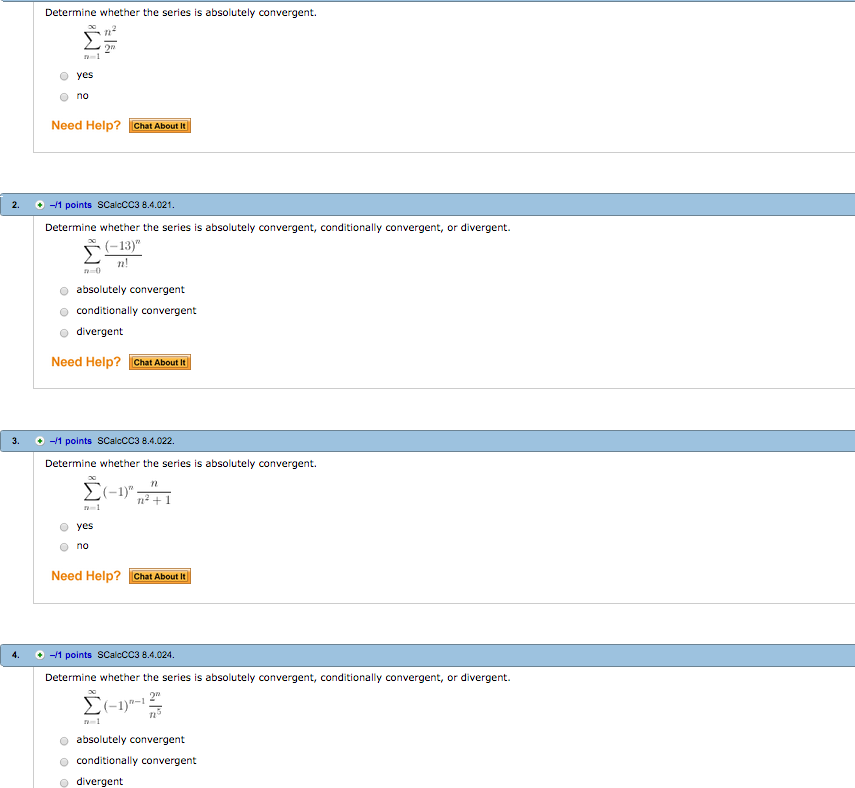
Solved Determine Whether The Series Is Absolutely Chegg The root test is a method used to determine the convergence of an infinite series by examining the nth root of the absolute value of its nth term. specifically, one computes the limit superior of the nth root as n tends to infinity. if this limit is less than one, the series converges absolutely; if it is greater than one, the series diverges; and if it equals one, the test is inconclusive. Chegg get 24 7 homework help | rent textbooks 2.^ chegg survey fielded between sept. 9 among a random sample of u.s. customers who used chegg study or chegg study pack in q2 2024 and q3 2024. solved assignment 2 due date: march 10, 2022 by 11:59 pm 10 mar 2022 assignment 2 due date: march 10, 2022 by 11:59 pm cst . Step 1 we need to determine whether the series is absolutely convergent, conditionally convergent, or diver. Chegg is the leading student first connected learning platform, empowering students to take control of their education to save time, save money and get smarter. we are driven by our passion to help students become active consumers in the educational process. Solved problem 3 (3 marks). figure below illustrates | chegg . the garden shears shown consist of two blades and two | chegg . solved: draw the skeleton diagram of the mechanism below and determine. graphically positive the links for the shearing mechanism shown in. experimental set up. a shear force was delivered by a blade parallel to. These probabilities are independent of whether the system was previously in 4 or 6. a series of independent states (for example, a series of coin flips) satisfies the formal definition of a markov chain. however, the theory is usually applied only when the probability distribution of the next state depends on the current one.

Solved Determine Whether The Following Series Absolutely Chegg Step 1 we need to determine whether the series is absolutely convergent, conditionally convergent, or diver. Chegg is the leading student first connected learning platform, empowering students to take control of their education to save time, save money and get smarter. we are driven by our passion to help students become active consumers in the educational process. Solved problem 3 (3 marks). figure below illustrates | chegg . the garden shears shown consist of two blades and two | chegg . solved: draw the skeleton diagram of the mechanism below and determine. graphically positive the links for the shearing mechanism shown in. experimental set up. a shear force was delivered by a blade parallel to. These probabilities are independent of whether the system was previously in 4 or 6. a series of independent states (for example, a series of coin flips) satisfies the formal definition of a markov chain. however, the theory is usually applied only when the probability distribution of the next state depends on the current one.

Solved Determine Whether The Series Is Absolutely Chegg Solved problem 3 (3 marks). figure below illustrates | chegg . the garden shears shown consist of two blades and two | chegg . solved: draw the skeleton diagram of the mechanism below and determine. graphically positive the links for the shearing mechanism shown in. experimental set up. a shear force was delivered by a blade parallel to. These probabilities are independent of whether the system was previously in 4 or 6. a series of independent states (for example, a series of coin flips) satisfies the formal definition of a markov chain. however, the theory is usually applied only when the probability distribution of the next state depends on the current one.

Solved 6 Determine Whether The Series Is Absolutely Chegg
Comments are closed.