Solved E And F Are Sets Of Real Numbers Defined As Follows Chegg

Solved E And F Are Sets Of Real Numbers Defined As Follows Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: e and f are sets of real numbers defined as follows. e = {x | x < 4} f = {x | x > 1| write e intersection f and e union f using interval notation. if the set is empty, write phi. e intersection f = e union f = here’s the best way to solve it. Set e represents all real numbers greater than 4. in interval notation, this is expressed as: set f represents all real numbers greater than or equal to 5. in interval notation, this is expressed as: the union of two sets, e ∪ f, includes all elements that are in either set e or set f.

Solved Question Chegg Maria g. asked • 07 19 19 e and f are sets of real numbers defined as follows. e= {w│w < 2} f= {w│w ≤ 5} write e u f and e ∩ f using interval notation. if the set is empty, write Ø. To solve this problem, we need to understand the definitions of union ($\cup$) and intersection ($\cap$) of sets, as well as how to express sets of real numbers in interval notation. The answer does not seem fully correct. the e u f= ( \infty , \infty ). that is not the answer you provided. but thank you. tutor. The union of two sets includes all the elements that are in either set. e = {w | w^2 ≤ 2} f = {w | w < 9} to find e u f, we need to combine the conditions of both sets.

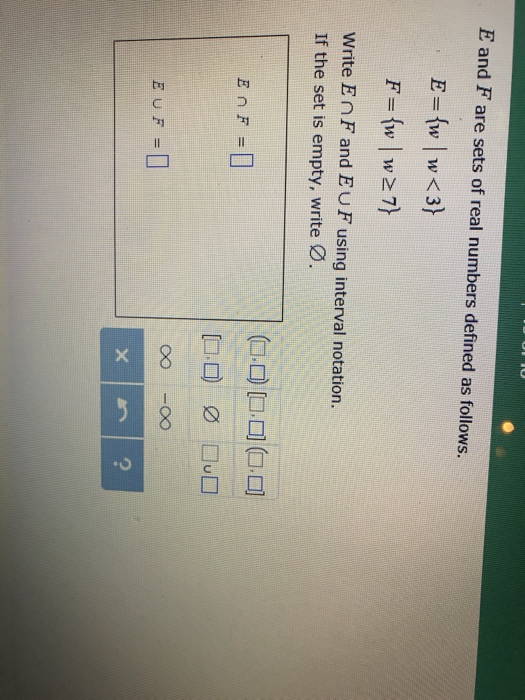
Solved E And F Are Sets Of Real Numbers Defined As Follows Chegg The answer does not seem fully correct. the e u f= ( \infty , \infty ). that is not the answer you provided. but thank you. tutor. The union of two sets includes all the elements that are in either set. e = {w | w^2 ≤ 2} f = {w | w < 9} to find e u f, we need to combine the conditions of both sets. E and f are sets of real numbers defined as follows. e = {z | z≤ 4} f = {z | z>8} write euf and enf using interval notation. if the set is empty, write Ø. euf = enf: = 0 (0,0) (0,0) Ø ∞ [0,0] (0,0) x 8 quo $ your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. The intersection of two sets e and f is the set of elements that are common to both e and f. since e = (−∞,1] and f = (−∞,8), we are looking for the numbers that satisfy both conditions: z ≤ 1 and z <8. Write e u f and e ∩ f using interval notation. if the set is empty, write Ø. e ∪ f in interval notation is ( ∞,∞). the union of the two sets means it includes every value less than 4, equal to 4, and greater than 4. e ∩ f is ∅. this is asking for the intersection of the two sets. E and f are sets of real numbers defined as follows. e= tyly<4) f= (y ly=6) write e u f and e n f using interval notation. if the set is empty, write (. euf = (0,0) [0,0] (0,0] [0,0) ovo enf = oo oo x 5 show more.