
Question Chegg Enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. there are 3 steps to solve this one. multiply the numerator and denominator of − 1 − 1 i 8 i by the conjugate of 8 i to make the denominator real. not the question you’re looking for? post any question and get expert help quickly. Evaluate the expression, and write the result as a simplified complex number.

Solved Evaluate The Expression 1 1i8i ï And Write The Result Chegg Get a free answer to a quick problem. most questions answered within 4 hours. choose an expert and meet online. no packages or subscriptions, pay only for the time you need. Your solution’s ready to go! enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. not the question you’re looking for? post any question and get expert help quickly. Evaluate the expression and write the result in the form a bi. just like rationalizing radical expressions, we evaluate the expression by multiplying the numerator and denominator by the denominator's complex conjugate and simplifying the expression until the form a b a b i bi is achieved. Simplify the expression: combine the constants and imaginary parts: − 1 − 1 = − 2. the imaginary part is zero: 0 i = 0. write the result in standard form: the expression simplifies to: − 2 0 i. so, the real number a equals − 2, and the real number b equals 0. thus, the evaluated expression (− 1 − 1 i) (1 − 1 i) in the form a.

Solved Evaluate The Expression 1 1i8i ï And Write The Result Chegg Evaluate the expression and write the result in the form a bi. just like rationalizing radical expressions, we evaluate the expression by multiplying the numerator and denominator by the denominator's complex conjugate and simplifying the expression until the form a b a b i bi is achieved. Simplify the expression: combine the constants and imaginary parts: − 1 − 1 = − 2. the imaginary part is zero: 0 i = 0. write the result in standard form: the expression simplifies to: − 2 0 i. so, the real number a equals − 2, and the real number b equals 0. thus, the evaluated expression (− 1 − 1 i) (1 − 1 i) in the form a. To evaluate the expression (− 1 3 i) (1 − i) and write the result in the form a bi, we can follow these steps: distribute each term of the first complex number to each term of the second complex number: multiply − 1 by 1, which gives − 1. multiply − 1 by − i, which gives i. multiply 3 i by 1, which gives 3 i. multiply 3 i by −. Here’s the best way to solve it. this ai generated tip is based on chegg's full solution. sign up to see more! rewrite the given expression 1 3 i 8 i and then multiply both the numerator and the denominator by the conjugate of the denominator. evaluate the expression 1 3i 8i and write the result in the form a bi. Answer to solved evaluate the expression (1 i)( 4 i) and write the | chegg. To evaluate the expression 7 i 1 − 3 i and write the result in the form a bi, follow these steps: identify the given expression: the expression is 7 i 1 − 3 i . multiply by the conjugate: to simplify the expression, we multiply both the numerator and the denominator by the conjugate of the denominator.
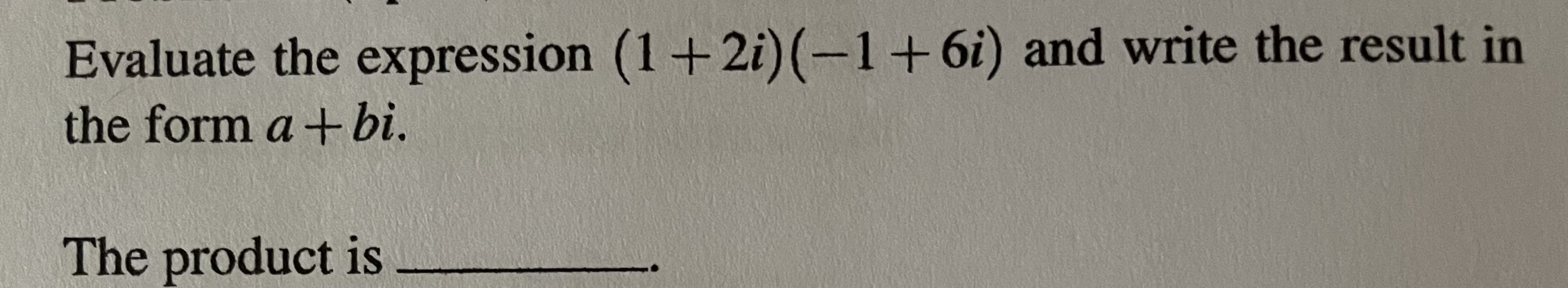
Solved Evaluate The Expression 1 2i 1 6i ï And Write The Chegg To evaluate the expression (− 1 3 i) (1 − i) and write the result in the form a bi, we can follow these steps: distribute each term of the first complex number to each term of the second complex number: multiply − 1 by 1, which gives − 1. multiply − 1 by − i, which gives i. multiply 3 i by 1, which gives 3 i. multiply 3 i by −. Here’s the best way to solve it. this ai generated tip is based on chegg's full solution. sign up to see more! rewrite the given expression 1 3 i 8 i and then multiply both the numerator and the denominator by the conjugate of the denominator. evaluate the expression 1 3i 8i and write the result in the form a bi. Answer to solved evaluate the expression (1 i)( 4 i) and write the | chegg. To evaluate the expression 7 i 1 − 3 i and write the result in the form a bi, follow these steps: identify the given expression: the expression is 7 i 1 − 3 i . multiply by the conjugate: to simplify the expression, we multiply both the numerator and the denominator by the conjugate of the denominator.
