
Solved Exercise 2 15 Prove The Following Two Relations Chegg Prove the identity (a b)2 = a 2 2ab 62 for all natural numbers a, b. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Prove the following set identities, using either venn diagrams or the rules of sets. a. [2] . a ∩ (b − a) = ∅ b. [2] (a ∩ b) ∪ (a ∩ b) = a c. [2] (a − b) − c ⊆ a − c d. [2] (a − c) ∩ (c − b) = ∅ e. argue that the symmetric difference operator does, or does not, always satisfy the associative property. list the elements in the following sets.
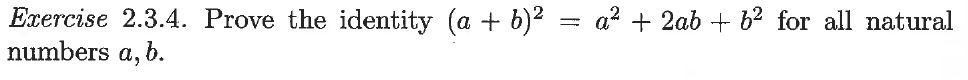
Solved Exercise 2 3 4 Prove The Identity A B 2 A 2 Chegg I was rereading terence tao's analysis 1 and found this question in the section: exercise $2.3.4.$ prove the identity $(a b)^2 = a^2 2ab b^2$ for all natural numbers a, b. prior to this we. Prove the identity \((a b)^2=a^2 2ab b^2\) for all natural numbers \(a,b\). \(\bullet\) show that \((a b)^2=a^2 2ab b^2\) for all natural numbers \(a,b\) . \(\vdash\) \((a b)^2\). $\begingroup$ a combinatorial proof is usually understood as one that establishes equality by counting the same group of things in two different ways. here the whole square is $(a b)^2$ and the four regions are $a^2,b^2,ab,ab$ $\endgroup$. Exercise 2.3.4 .prove the identity (a b)^2=a^2 2ab b^2 for all natural numbers a, b. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.
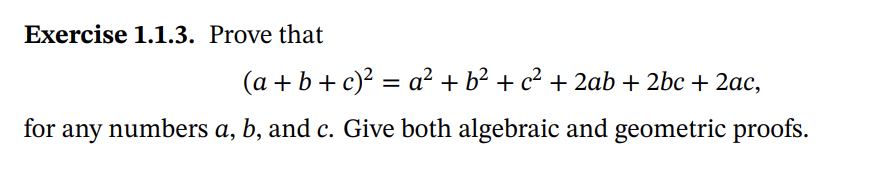
Solved Exercise 1 1 3 Prove That Chegg $\begingroup$ a combinatorial proof is usually understood as one that establishes equality by counting the same group of things in two different ways. here the whole square is $(a b)^2$ and the four regions are $a^2,b^2,ab,ab$ $\endgroup$. Exercise 2.3.4 .prove the identity (a b)^2=a^2 2ab b^2 for all natural numbers a, b. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Algebraic identity (a b) 2 = a 2 2ab b 2 is verified. the identity (a b) 2 = a 2 2ab b 2 is verified by cutting and pasting of paper. this identity can be verified geometrically by taking other values of a and b. divide a square plot into four parts (quadrilaterals) such that two parts have same area and other two are squares. viva voce. To verify the identity (a² – b²) = (a b) (a b) (method 2) materials required. we take any values of a and b such that a>b. step 1: construct a square abcd on the glazed paper such that each side of this square measures a units. inside this square construct another square aefg of side b units (where b < a) as shown in figure 9.1. join fc. In this method, substitute the values for the variables and perform the arithmetic operation. another method to verify the algebraic identity is the activity method. in this method, you would need a prerequisite knowledge of geometry and some materials are needed to prove the identity. In an identity (a – b)² =a² b² – 2ab, if both variables are equal, then find the value of (a – b)². answer: when a = b, then (a b)² = (b b)² =0. suggested activity verify the algebraic identity (a b)² = a² – 2ab b² by taking a = 9 and b = 4. math labs math labs with activity math lab manual science labs science practical skills.
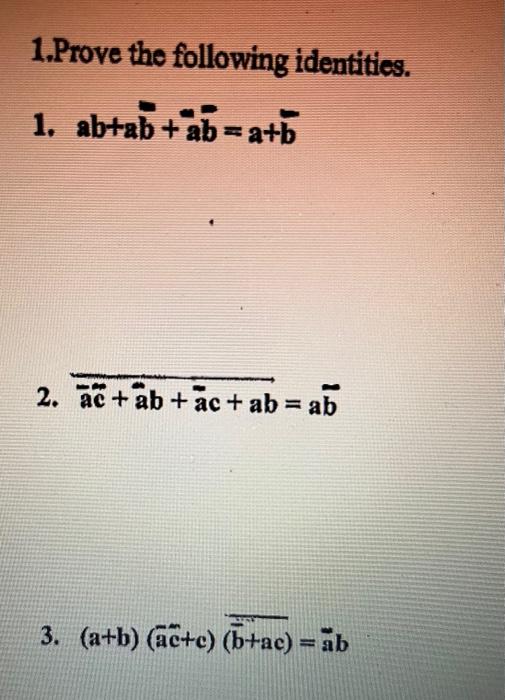
Solved 1 Prove The Following Identities 1 Ab Ab Abˉ A Bˉ Chegg Algebraic identity (a b) 2 = a 2 2ab b 2 is verified. the identity (a b) 2 = a 2 2ab b 2 is verified by cutting and pasting of paper. this identity can be verified geometrically by taking other values of a and b. divide a square plot into four parts (quadrilaterals) such that two parts have same area and other two are squares. viva voce. To verify the identity (a² – b²) = (a b) (a b) (method 2) materials required. we take any values of a and b such that a>b. step 1: construct a square abcd on the glazed paper such that each side of this square measures a units. inside this square construct another square aefg of side b units (where b < a) as shown in figure 9.1. join fc. In this method, substitute the values for the variables and perform the arithmetic operation. another method to verify the algebraic identity is the activity method. in this method, you would need a prerequisite knowledge of geometry and some materials are needed to prove the identity. In an identity (a – b)² =a² b² – 2ab, if both variables are equal, then find the value of (a – b)². answer: when a = b, then (a b)² = (b b)² =0. suggested activity verify the algebraic identity (a b)² = a² – 2ab b² by taking a = 9 and b = 4. math labs math labs with activity math lab manual science labs science practical skills.
