
Solved Exercises 2 1 Let A1 2 A2 4 And An 1 Chegg Question: exercises .2 1. let a1 = 2, a2 = 4, and an 1 = 7a, 10an 1 for all n 2. let a1 = 3, a2 4, and an 1 = (2an an 1) for all n 2. prove that for all 3. without using the fundamental theorem of arithmetic, use strong induction 4. for i e z , let pi denote the ith prime number, so that 2. Identify the solution of the recurrence relation an = 6 an − 1 – 8 an − 2 for n ≥ 2 together with the initial conditions a 0 = 4 and a 1 = 10. solve these recurrence relations together with the initial conditions given.

Solved 1 Let A1 1 2 3 4 A2 0 1 2 A3 1 0 1 And Let Chegg 1. let a1 = 2, a2 4, and an 1 = 7an 10an 1 for all n > 2, conjecture a closed formula for an and then prove your result. Conjecture a closed formula for an and then prove your result. 2. let a1 =3,a2 =4, and an 1 =31 (2an an−1 ) for all n≥2. prove that for all positive integers n,3≤an ≤4. 3. without using the fundamental theorem of arithmetic, use strong induction to prove that for all positive integers n with n≥2,n has a prime factor. Let a1=2, a2=4, and an 2=5 an 1 6 an for all n ≥ 1 . prove that an=2^n for all natural numbers n . thus, as shown, a m=2^m. hence, by pci, the statement is true for all natural numbers greater than or equal to 1. how would you rate this answer and explanation? let a1=2, a2=4, and an 2=5 an 1 6 an for all n ≥ 1 . Answer: (i) to prove that p (a1 a2) p (a1) we take p (a1 a2) = ∩ ≤ ∩ p (a2|a1)p (a1) dividing throughout by p (a2|a1) gives (a1 = a2) ∩ p (a1 a (a2|a1) ≥ ∩ since p (a2|a1) 1.

Only Questions Underlined In Red1 1 3 4 2 5 Chegg Let a1=2, a2=4, and an 2=5 an 1 6 an for all n ≥ 1 . prove that an=2^n for all natural numbers n . thus, as shown, a m=2^m. hence, by pci, the statement is true for all natural numbers greater than or equal to 1. how would you rate this answer and explanation? let a1=2, a2=4, and an 2=5 an 1 6 an for all n ≥ 1 . Answer: (i) to prove that p (a1 a2) p (a1) we take p (a1 a2) = ∩ ≤ ∩ p (a2|a1)p (a1) dividing throughout by p (a2|a1) gives (a1 = a2) ∩ p (a1 a (a2|a1) ≥ ∩ since p (a2|a1) 1. Ex 12.1, 29 let a1, a2,… , an be fixed real numbers and define a function f (x) = (x – a1) (x – a2)…. (x – an) what is lim┬ (x→a"1" ) f (x)? for some a ≠ a1, a2…… an, compute lim┬ (x→a) f (x). f (x) = (x – a1) (x – a2) ……. (x – an) calculating (𝐥𝐢𝐦)┬ (𝐱→𝐚"1" ) f (x) lim┬ (x→a"1" ) f (x. Arrange these steps of the linear search for finding location of an element x in a list a1, a2 , , a (n) 1. compare x and a1. 2. when = a1, the solution is 1 (the index of the term a). 3. otherwise, when x does not = a1, and the sequence does not end with a 1, compare x with a2. 4. if x = a2, the solution is the location of a2. Let a₁ = 2, a2 = 4, and an 1 7an 10an 1 for all n ≥ 2. conjecture a closed formula for an and then prove your result. = 2. let a₁ = 3, a2 = 4, and an 1 positive integers n, 3 ≤ an ≤ 4. (2an an 1) for all n ≥ 2. prove that for all 3. without using the fundamental theorem of arithmetic, use strong induction to prove that for all positive. Let a1,a2, ,an be events in the sample space Ω with probability measure p. show that a) p (a1 ∪ a2 ∪ · · · ∪ an) ≤ p (a1) p (a2) · · · p (an); b) p (a1 ∩ a2 ∩ · · · ∩ an) ≥ p (a1) p (a2).
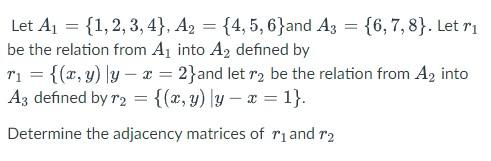
Solved Let A1 1 2 3 4 A2 4 5 6 And A3 6 7 8 Let R1 Be Chegg Ex 12.1, 29 let a1, a2,… , an be fixed real numbers and define a function f (x) = (x – a1) (x – a2)…. (x – an) what is lim┬ (x→a"1" ) f (x)? for some a ≠ a1, a2…… an, compute lim┬ (x→a) f (x). f (x) = (x – a1) (x – a2) ……. (x – an) calculating (𝐥𝐢𝐦)┬ (𝐱→𝐚"1" ) f (x) lim┬ (x→a"1" ) f (x. Arrange these steps of the linear search for finding location of an element x in a list a1, a2 , , a (n) 1. compare x and a1. 2. when = a1, the solution is 1 (the index of the term a). 3. otherwise, when x does not = a1, and the sequence does not end with a 1, compare x with a2. 4. if x = a2, the solution is the location of a2. Let a₁ = 2, a2 = 4, and an 1 7an 10an 1 for all n ≥ 2. conjecture a closed formula for an and then prove your result. = 2. let a₁ = 3, a2 = 4, and an 1 positive integers n, 3 ≤ an ≤ 4. (2an an 1) for all n ≥ 2. prove that for all 3. without using the fundamental theorem of arithmetic, use strong induction to prove that for all positive. Let a1,a2, ,an be events in the sample space Ω with probability measure p. show that a) p (a1 ∪ a2 ∪ · · · ∪ an) ≤ p (a1) p (a2) · · · p (an); b) p (a1 ∩ a2 ∩ · · · ∩ an) ≥ p (a1) p (a2).

Solved Let A1 1 2 3 4 A2 4 5 6 And A3 6 7 8 Let R1 Be Chegg Let a₁ = 2, a2 = 4, and an 1 7an 10an 1 for all n ≥ 2. conjecture a closed formula for an and then prove your result. = 2. let a₁ = 3, a2 = 4, and an 1 positive integers n, 3 ≤ an ≤ 4. (2an an 1) for all n ≥ 2. prove that for all 3. without using the fundamental theorem of arithmetic, use strong induction to prove that for all positive. Let a1,a2, ,an be events in the sample space Ω with probability measure p. show that a) p (a1 ∪ a2 ∪ · · · ∪ an) ≤ p (a1) p (a2) · · · p (an); b) p (a1 ∩ a2 ∩ · · · ∩ an) ≥ p (a1) p (a2).
