Solved F Maps 0 1 0 1 F X 0 If X Is Irrational And 1 Q Chegg
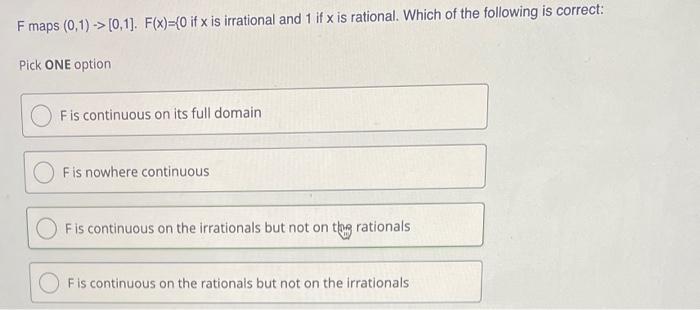
Solved F Maps 0 1 0 1 F X 0 If X Is Irrational And 1 Chegg Math advanced math advanced math questions and answers f maps (0,1) > [0,1]. f (x)= {0 if x is irrational and 1 q if x is rational with reduced form p q, for p & q relatively prime integers. The function f (x) is defined so that it takes the value 0 for irrational x and 1 q for rational x, where the rational number x is in reduced form p q and p and q are relatively prime.

Solved 1 Point Given And F 0 0 And F 0 1 Find Chegg F (x)= {0 if x is irrational and 1 q if x is rational with reduced form p a, for p & q relatively prime integers. Since the rational numbers are dense within the interval (0,1), there are infinitely many discontinuities in any neighborhood of any point. thus, f is not continuous at any point in its domain, making option b the correct choice. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer question: f maps (0,1)→ [0,1]. f (x)= (0 if x is irrational and 1 q if x is rational with reduced form p q, for p& q relatively prime integers. The question asks about the continuity of a function f (x) that maps the open interval (0,1) to the closed interval [0,1]. the function is defined as follows: f (x)=0 if x is irrational and f (x)=1 q if x is a rational number in reduced form p q, where p and q are relatively prime integers.

Solved F Maps 0 1 0 1 F X 0 If X Is Irrational And 1 Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer question: f maps (0,1)→ [0,1]. f (x)= (0 if x is irrational and 1 q if x is rational with reduced form p q, for p& q relatively prime integers. The question asks about the continuity of a function f (x) that maps the open interval (0,1) to the closed interval [0,1]. the function is defined as follows: f (x)=0 if x is irrational and f (x)=1 q if x is a rational number in reduced form p q, where p and q are relatively prime integers. F (x)= (0 if x is irrational and 1 if x is rational. which of the following is correct: pick one option f is continuous on its full domain f is nowhere continuous f is continuous on the irrationals but not on the rationals f is continuous on the rationals but not on the irrationals. Your statement about discontinuities at the endpoints doesn’t make sense: if one of the endpoints of the interval is included in $x$, then $f$ must be continuous there, and if one is not included, then $f$ isn’t even defined there and so cannot be discontinuous there. 00:01 hello students in this problem f is mapped from the open interval 0 ,1 to the close interval 0 ,1 and here the function is defined as f of x is equal to 0 and 1 by q 0 if x is irrational 1 by q if x is rational and from the given option the correct answer is option b f is nowhere continuous. Problem: let $i= [0,1]$ be the closed unit interval. suppose $f$ is a continuous mapping of $i$ into $i$. prove that $f (x)=x$ for at least one $x \in i$. attempt: we have a known result: let $.

Solved Consider The Function F 0 1 Right Arrow R Defined Chegg F (x)= (0 if x is irrational and 1 if x is rational. which of the following is correct: pick one option f is continuous on its full domain f is nowhere continuous f is continuous on the irrationals but not on the rationals f is continuous on the rationals but not on the irrationals. Your statement about discontinuities at the endpoints doesn’t make sense: if one of the endpoints of the interval is included in $x$, then $f$ must be continuous there, and if one is not included, then $f$ isn’t even defined there and so cannot be discontinuous there. 00:01 hello students in this problem f is mapped from the open interval 0 ,1 to the close interval 0 ,1 and here the function is defined as f of x is equal to 0 and 1 by q 0 if x is irrational 1 by q if x is rational and from the given option the correct answer is option b f is nowhere continuous. Problem: let $i= [0,1]$ be the closed unit interval. suppose $f$ is a continuous mapping of $i$ into $i$. prove that $f (x)=x$ for at least one $x \in i$. attempt: we have a known result: let $.
Comments are closed.