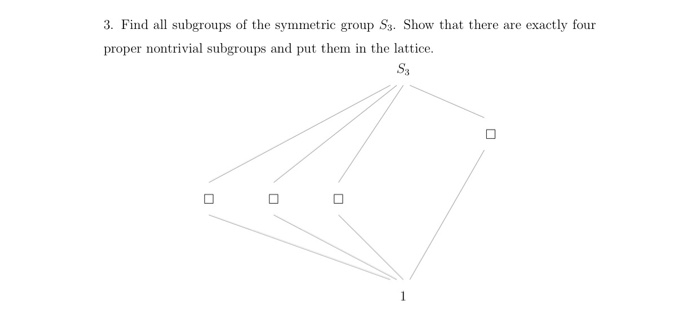
Solved 3 Find All Subgroups Of The Symmetric Group S3 Show Chegg Math advanced math advanced math questions and answers 4. find all subgroups of s3, the symmetric group of degree 3. To get started, identify the elements of the symmetric group s 3 and recognize that the order of s 3 is 6 since | s 3 | = 3! = 6.
Solved Find All Subgroups Of S3 The Symmetric Group Chegg So by enumerating cyclic subgroups we have obtain list of all proper subgroups of s3 s 3. we can check our result at groupprops wiki (or elsewhere): subgroup structure of symmetric group:s3. So i know that all subgroups must have 1 (trivial), 2, 3, or 6 (trivial) elements. we could proceed with further analysis, such as the fact that the standard 3 cycle must have order 3, and so if it is a member of a subgroup (which it is) then that subgroup's order must be divisible by 3. To find all subgroups of s3 s 3, the symmetric group of degree 3, we first need to understand the structure of s3 s 3. ### symmetric group of degree 3 the symmetric group sn s n consists of all permutations of n n elements. for s3 s 3, we have 3 elements: {1, 2, 3} {1, 2, 3}. Exercise 3.23 find all subgroups of the symmetric group s3. which of them are normal subgroups? [ss is the group of all permutations of (1,2,3).] your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: exercise 3.23 find all subgroups of the symmetric group s3.
Solved 4 Find All Subgroups Of S3 The Symmetric Group Of Chegg To find all subgroups of s3 s 3, the symmetric group of degree 3, we first need to understand the structure of s3 s 3. ### symmetric group of degree 3 the symmetric group sn s n consists of all permutations of n n elements. for s3 s 3, we have 3 elements: {1, 2, 3} {1, 2, 3}. Exercise 3.23 find all subgroups of the symmetric group s3. which of them are normal subgroups? [ss is the group of all permutations of (1,2,3).] your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: exercise 3.23 find all subgroups of the symmetric group s3. If you regard the elements of your s4 as acting on the elements {1,2,3,4} of s, then the don't act on {5,6} at all. 5 and 6 are fixed. you could take your subgroup of order 8 and add a permutation to it that doesn't fix {5,6} to make a larger group. Now, let's find all subgroups of s3. we know that any subgroup must contain the identity element (), and it must be closed under multiplication and inversion. we can start by considering the subgroups generated by each element of s3: the subgroup generated by () is just { ()}. the subgroup generated by (1 2) is { (), (1 2)}. Here’s the best way to solve it. as per theorem order of any subgroup m … not the question you’re looking for? post any question and get expert help quickly. Find the longest common subsequence (lcs) of the sequences x =< acbac > and y =< aabc >. fill out the 2d array c [0.m, 0.n], where c [i, j] is defined to be the length.

Solved 20 Points Consider The Group S3 Symmetric Group On Chegg If you regard the elements of your s4 as acting on the elements {1,2,3,4} of s, then the don't act on {5,6} at all. 5 and 6 are fixed. you could take your subgroup of order 8 and add a permutation to it that doesn't fix {5,6} to make a larger group. Now, let's find all subgroups of s3. we know that any subgroup must contain the identity element (), and it must be closed under multiplication and inversion. we can start by considering the subgroups generated by each element of s3: the subgroup generated by () is just { ()}. the subgroup generated by (1 2) is { (), (1 2)}. Here’s the best way to solve it. as per theorem order of any subgroup m … not the question you’re looking for? post any question and get expert help quickly. Find the longest common subsequence (lcs) of the sequences x =< acbac > and y =< aabc >. fill out the 2d array c [0.m, 0.n], where c [i, j] is defined to be the length.
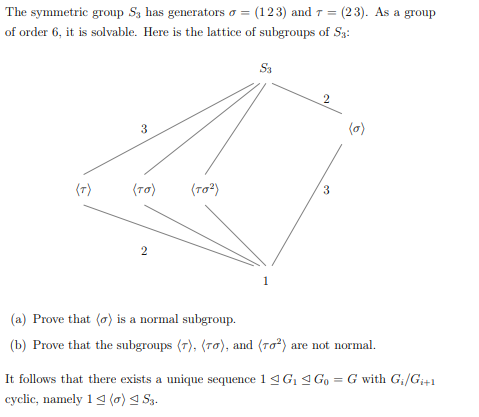
Solved The Symmetric Group S3 Has Generators σ 123 And Chegg Here’s the best way to solve it. as per theorem order of any subgroup m … not the question you’re looking for? post any question and get expert help quickly. Find the longest common subsequence (lcs) of the sequences x =< acbac > and y =< aabc >. fill out the 2d array c [0.m, 0.n], where c [i, j] is defined to be the length.
