Solved Find All Vectors U Which Are Orthogonal To The Vector V
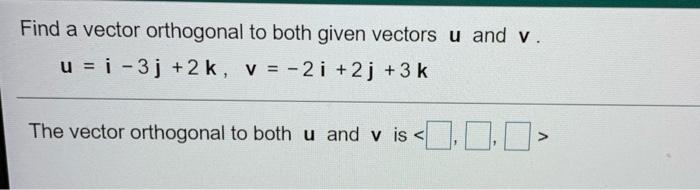
Solved Find A Vector Orthogonal To Both Given Vectors U And Chegg I'm currently in a linear algebra course and i am just looking for feedback or some sort of verification of what i'm doing is correct. so i have to find all vectors that are orthogonal to $u= (1,. The dot product of vectors u u u and v v v is given by x ∗ 1 y ∗ 2 z ∗ (− 1) x*1 y*2 z* ( 1) x∗1 y∗2 z∗(−1). two vectors are orthogonal if their dot product is zero.

Solved Find A Vector Orthogonal To Both Given Vectors U And Chegg To determine all vectors v that are orthogonal to a given vector u, we set the dot product of u and v to be zero. solving for a component of v, such as v2, gives us v2 = 8t. Our exercise specifically asks us to find all vectors orthogonal to a given vector u. using the definition from linear algebra, we employ the dot product to find all vectors v that satisfy the criterion for orthogonality. we set up the equation u v = 0 and solve for v to find all possible solutions. To find all vectors in $\mathbb {r}^4$ that are orthogonal to the vectors $\mathbf {u}$, $\mathbf {v}$, and $\mathbf {w}$, we need to find a vector $\mathbf {x} = (x 1, x 2, x 3, x 4)$ such that the dot product of $\mathbf {x}$ with each of $\mathbf {u}$, $\mathbf {v}$, and $\mathbf {w}$ is zero. In this section, we examine what it means for vectors (and sets of vectors) to be orthogonal and orthonormal. recall from the properties of the dot product of vectors that two vectors \ (\vec {u}\) and \ (\vec {v}\) are orthogonal if \ (\vec {u} \cdot \vec {v} = 0\). suppose a vector is orthogonal to a spanning set of \ (\mathbb {r}^n\). what can be said about such a vector? this is the.

Solved Two Vectors U And V Are Given A Find A Vector Chegg To find all vectors in $\mathbb {r}^4$ that are orthogonal to the vectors $\mathbf {u}$, $\mathbf {v}$, and $\mathbf {w}$, we need to find a vector $\mathbf {x} = (x 1, x 2, x 3, x 4)$ such that the dot product of $\mathbf {x}$ with each of $\mathbf {u}$, $\mathbf {v}$, and $\mathbf {w}$ is zero. In this section, we examine what it means for vectors (and sets of vectors) to be orthogonal and orthonormal. recall from the properties of the dot product of vectors that two vectors \ (\vec {u}\) and \ (\vec {v}\) are orthogonal if \ (\vec {u} \cdot \vec {v} = 0\). suppose a vector is orthogonal to a spanning set of \ (\mathbb {r}^n\). what can be said about such a vector? this is the. This method of finding orthogonal vectors relies on the definition of the dot product in vector mathematics, which states that two vectors are orthogonal if their dot product results in zero. Enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. not the question you’re looking for? post any question and get expert help quickly. Determine all vectors v that are orthogonal to u. (set v1 = t and v3 = s and solve for v2 in terms of t and s.). If i have a vector v = 3, 4, 0 v → = 3, 4, 0 , and want to find all unit vectors which are orthogonal to v v →, i am interested in how to best go about determining this solution set, or even a single member of the solution set.

Solved Find A Vector Orthogonal To Both Given Vectors U And Chegg This method of finding orthogonal vectors relies on the definition of the dot product in vector mathematics, which states that two vectors are orthogonal if their dot product results in zero. Enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. not the question you’re looking for? post any question and get expert help quickly. Determine all vectors v that are orthogonal to u. (set v1 = t and v3 = s and solve for v2 in terms of t and s.). If i have a vector v = 3, 4, 0 v → = 3, 4, 0 , and want to find all unit vectors which are orthogonal to v v →, i am interested in how to best go about determining this solution set, or even a single member of the solution set.
Comments are closed.