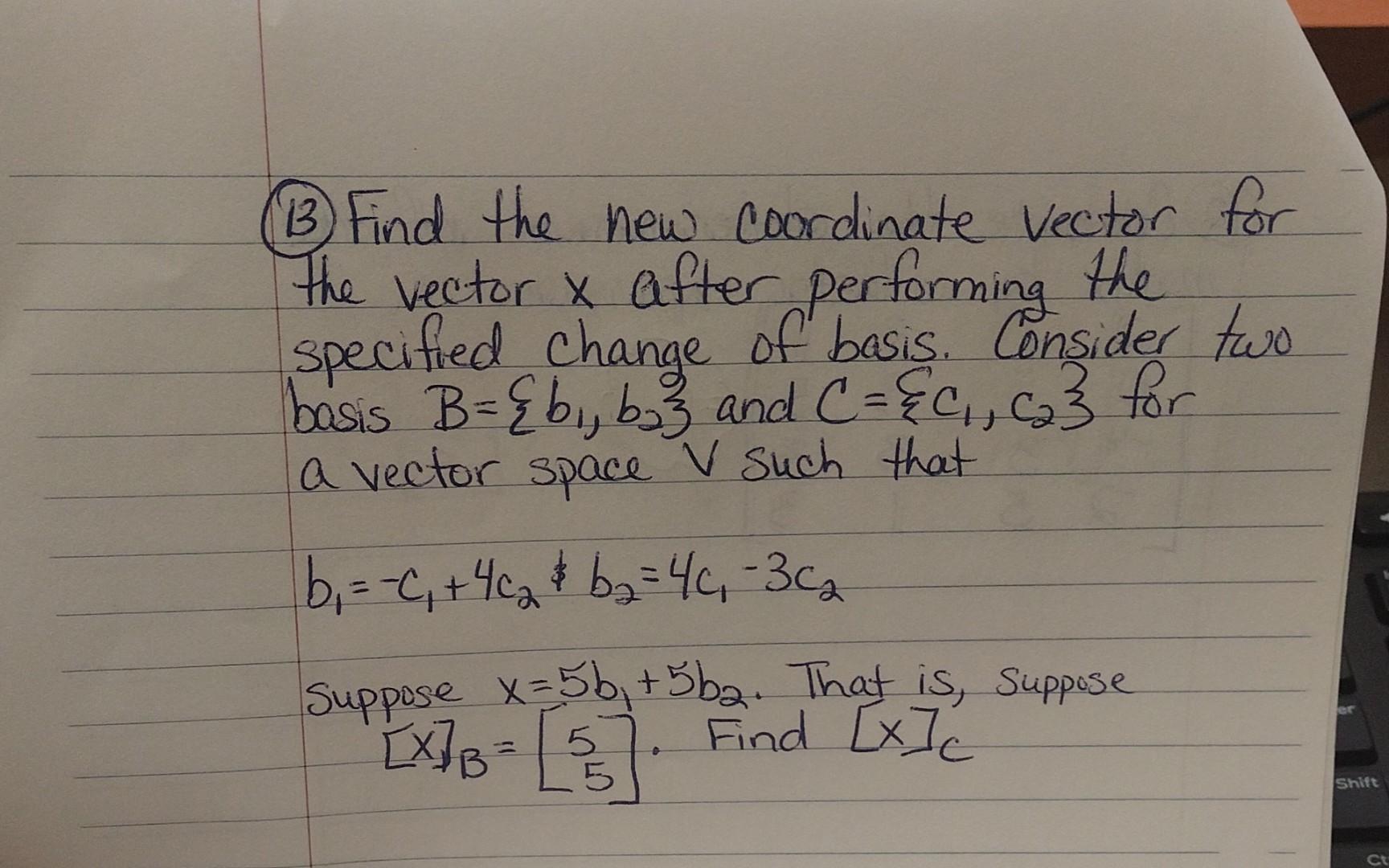
Solved B Find The New Coordinate Vector For The Vector X Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. there are 3 steps to solve this one. find the coordinate vector x → = [3 − 5] of the vector relative to the basis b = {b → 1, b → 2} . not the question you’re looking for? post any question and get expert help quickly. I understand how to find the coordinate vector when the basis is composed of two 2 x 1 matrices. but when they have a higher order i struggle. i would begin this problem by setting up a matrix equation in the form $ax = b$.

Solved Find The Coordinate Vector X B Of The Vector X Chegg There are 3 steps to solve this one. 2. find the coordinate vector [x]b of x relative to the given basis b = {b1, , bn}. 2 (a) bi = b2 = ,x= 2 0 (b) b1 = ,b3 = , x= 0 1,b2 = 3 1 3 8 3. use an inverse matrix to find [x]b for the given x and b. 1 3 (8 1365 { {11 13)} e { [ 2] [**]},x= [23] = [] [= [1] a) b= , x (b) b = 5. First, we need to express the vector x in terms of the basis vectors b1, b2, and b3. let's assume that x can be written as a linear combination of these basis vectors: x = c1 * b1 c2 * b2 c3 * b3 now, we need to find the coefficients c1, c2, and c3. to do this, we can set up a system of linear equations using the components of x and the. To find the coordinate vector [x]b of vector x relative to the basis b, we need to express x as a linear combination of b1 and b2, and then solve for the coefficients. let x be a vector of the form x = [x1 x2 x3]. then we can write: x = c1 b1 c2 b2 . where c1 and c2 are coefficients to be determined. To find the vector x x, we need to express the given coordinate vector [x] x] b b in terms of the given basis b b. 1 for each component of x x, multiply the corresponding component of the basis vector by the corresponding component of the coordinate vector. 2 calculate the resulting vector.

Solved Find The Coordinate Vector X B Of The Vector X Chegg To find the coordinate vector [x]b of vector x relative to the basis b, we need to express x as a linear combination of b1 and b2, and then solve for the coefficients. let x be a vector of the form x = [x1 x2 x3]. then we can write: x = c1 b1 c2 b2 . where c1 and c2 are coefficients to be determined. To find the vector x x, we need to express the given coordinate vector [x] x] b b in terms of the given basis b b. 1 for each component of x x, multiply the corresponding component of the basis vector by the corresponding component of the coordinate vector. 2 calculate the resulting vector. (a) use the basis $b=\{1, x, x^2\}$ of $p 2$, give the coordinate vectors of the vectors in $q$. (b) find a basis of the span $\span(q)$ consisting of vectors in $q$. (c) for each vector in $q$ which is not a basis vector you obtained in (b), express the vector as a linear combination of basis vectors. In exercises $1 4,$ find the vector $\mathbf{x}$ determined by the given coordinate vector $[\mathbf{x}] {\mathcal{b}}$ and the given basis $\mathcal{b} .$ \mathcal{b}=\left\{\left[\begin{array}{r}{3} \\ { 5}\end{array}\right],\left[\begin{array}{r}{ 4} \\ {6}\end{array}\right]\right\},[\mathbf{x}] {\mathcal{b}}=\left[\begin{array}{l}{5} \\ {3. Our expert help has broken down your problem into an easy to learn solution you can count on. there are 4 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. Coordinate vectors are [3, − 7] for b and [− 1, − 4] for c; [x] ∞ confirms [− 1, − 5]. the basis b is {[1 0], [1 1]}. to find [x] b, solve the equation [1 1 0 1] [a b] = [3 − 4] using the formula a ⋅ [1 0] b ⋅ [1 1] = [3 − 4]. solving this, [x] b = [3 − 7]. the basis c is {[1 − 1], [0 1]}.

Solved Find The Coordinate Vector X B Of The Vector Chegg (a) use the basis $b=\{1, x, x^2\}$ of $p 2$, give the coordinate vectors of the vectors in $q$. (b) find a basis of the span $\span(q)$ consisting of vectors in $q$. (c) for each vector in $q$ which is not a basis vector you obtained in (b), express the vector as a linear combination of basis vectors. In exercises $1 4,$ find the vector $\mathbf{x}$ determined by the given coordinate vector $[\mathbf{x}] {\mathcal{b}}$ and the given basis $\mathcal{b} .$ \mathcal{b}=\left\{\left[\begin{array}{r}{3} \\ { 5}\end{array}\right],\left[\begin{array}{r}{ 4} \\ {6}\end{array}\right]\right\},[\mathbf{x}] {\mathcal{b}}=\left[\begin{array}{l}{5} \\ {3. Our expert help has broken down your problem into an easy to learn solution you can count on. there are 4 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. Coordinate vectors are [3, − 7] for b and [− 1, − 4] for c; [x] ∞ confirms [− 1, − 5]. the basis b is {[1 0], [1 1]}. to find [x] b, solve the equation [1 1 0 1] [a b] = [3 − 4] using the formula a ⋅ [1 0] b ⋅ [1 1] = [3 − 4]. solving this, [x] b = [3 − 7]. the basis c is {[1 − 1], [0 1]}.

Solved Find The Coordinate Vector X B Of The Vector X Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. there are 4 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. Coordinate vectors are [3, − 7] for b and [− 1, − 4] for c; [x] ∞ confirms [− 1, − 5]. the basis b is {[1 0], [1 1]}. to find [x] b, solve the equation [1 1 0 1] [a b] = [3 − 4] using the formula a ⋅ [1 0] b ⋅ [1 1] = [3 − 4]. solving this, [x] b = [3 − 7]. the basis c is {[1 − 1], [0 1]}.

Solved Find The Coordinate Vector X B Of The Vector X Chegg
